Динамика. Механические колебания и волны апрель 2020г.

Динамика. Механические колебания и волны апрель 2020г.

Дайте определения следующих понятий: Дайте определения следующих величин:

1. Инерциальной системы отсчета (ИСО); 2. Системы материальных точек (СМТ); 3. Веса тела; 4. Замкнутой системы; 5. Консервативной силы; 6. Диссипативной силы; 7. Гироскопической силы; 8. Упругого столкновения; 9. Неупругого столкновения; 10. Центрального столкновения; 11. Нецентрального столкновения; 12. Механических колебаний (МК); 13. Кинематического уравнения МК; 14. Свободных МК; 15. Вынужденных МК; 16. Явления механического резонанса; 17. Резонансной частоты; 18. Резонансной амплитуды; 19. Волнового движения (волны); 20. Луча; 21. Поперечной волны; (илл) 22. Продольной волны; (илл) 23. Уравнения механической волны; 24. Фронта волны; (илл) 25. Вектора Умова-Пойтинга;

Силы,
Массы;
Импульса МТ
Импульса СМТ;
Равнодействующей силы;
Результирующей силы;
Напряжения деформированного тела;
Механической работы силы;
Мощности;
Момента силы относительно точки;(илл)
Момента силы относительно оси; (илл)
Вращающего момента;
Момента инерции МТ относительно оси;
Момента инерции СМТ относительно оси;
Момента импульса МТ относительно точки (илл)
Момента импульса МТ относительно оси; (илл)
Момента импульса СМТ относительно точки
Момента импульса СМТ относительно оси;
Периода МК; (илл)
Линейной частоты МК;
Циклической частоты МК;
Фазы колебаний;
Коэффициента затухания;
Декремента затухания;
Логарифмического декремента затухания;
Длины волны;(илл)
Объёмной плотности энергии;
Потока энергии;
Плотности потока энергии;
Интенсивности волны.

II. Сформулируйте:

1. Первый закон Ньютона.

2. Второй закон Ньютона.

3. Третий закон Ньютона. (илл)

4. Теорему об изменении импульса СМТ (и следствия из неё).

5. Теорему об изменении момента импульса центра масс.

6. Закон всемирного тяготения. (илл)

7. Физический смысл гравитационной постоянной.

8. Закон Гука (в первой форме).

9. Физический смысл коэффициента жёсткости.

10. Закон Гука (во второй форме).

11. Физический смысл модуля Юнга.

12. Закон Кулона-Амонтона.

13. Закон изменения кинетической энергии.

14. Закон изменения потенциальной энергии.

15. Физический смысл кинетической энергии.

16. Физический смысл потенциальной энергии.

17. Закон изменения полной механической энергии.

18. Закон сохранения полной механической энергии.

19. Смысл основного уравнения динамики вращательного движения.

20. Условия возникновения свободных незатухающих МК.

21. Условия возникновения свободных затухающих МК.

22. Условия возникновения вынужденных МК.

23. Сущность эффекта Доплера.

III. Доказательства

1. Выведите теорему об изменении импульса СМТ. Следствия из неё. (илл)

2. Исходя из закона всемирного тяготения, получите выражение для ускорения свободного падения и проанализируйте его. (илл)

3. Докажите, что вес тела, движущегося равномерно прямолинейно, численно равен силе тяжести (P=mg).(илл)

4. Используя две формы записи закона Гука, получите связь коэффициента жёсткости и модуля Юнга.

5. Исходя из определения механической работы, получите закон изменения кинетической энергии.(илл)

6. Получите формулу для расчёта работы силы тяжести.(илл)

7. Получите формулу для расчёта работы силы упругости (аналитический и графический метод). (илл)

8. Получите закон изменения полной механической энергии. Следствия из него.

9. Получите дифференциальное (и запишите кинематическое) уравнение гармонических МК (на примере колебаний груза на пружине).(илл)

10. Получите дифференциальное (и запишите кинематическое) уравнение гармонических МК (на примере колебаний математического маятника). (илл)

11. Используя кинематическое уравнения гармонических колебаний материальной точки x=x_maxcos(ω_оt+φ_ох), получите закон изменения линейной скорости МТ v(t) и соотношение между фазами φ_ох и φ_оv

12. Используя кинематическое уравнения гармонических колебаний материальной точки x=x_maxcos(ω_оt+φ_ох), получите закон изменения линейного ускорения МТ a(t)и соотношение между фазами φ_ох и φ_оa

13. Покажите справедливость закона сохранения полной механической энергии при гармонических МК.

14. Получите дифференциальное уравнение затухающих МК (на примере колебаний груза на пружине). (илл)

15. Получите связь логарифмического декремента затухания λ и коэффициента затухания β (λ=βT).

16. Используя выражение для амплитуды вынужденных колебаний 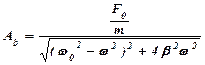, получите выражение для резонансной частоты и резонансной амплитуды.

17. Получите уравнение механической волны x=Asin(ωt-ωr/v+φ_ох). Смысл величин, входящих в уравнение. (илл)

18. Получите формулу для расчёта интенсивности механической волны. (илл.)