Сложение и вычитание векторов

Сложение и вычитание векторов

Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями

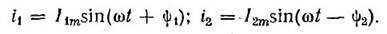
Сложим два заданных токаi1 иi2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:

I_m = I_m1 + I_m2

Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.

Вектор I_m, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).

Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):

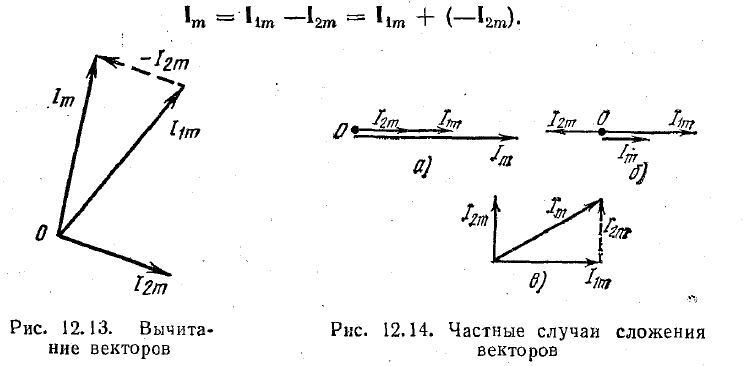
При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.

Попробуйте построить вектора

u = 300 sin(ωt + П/4)

i = 6 sin(ωt — П/3).

⇐ Предыдущая 1 23