Методы решения тригонометрических уравнений.

Методы решения тригонометрических уравнений.

Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида ( см. выше ) и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.

1. Алгебраический метод.

Этот метод нам хорошо известен из алгебры

( метод замены переменной и подстановки ).

2. Разложение на множители.

Этот метод рассмотрим на примерах.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

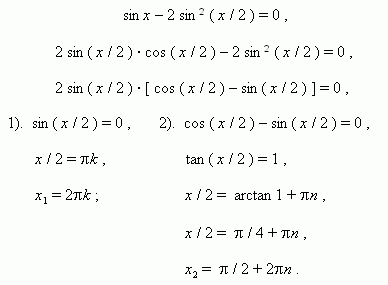
П р и м е р 2. Решить уравнение: cos ² x + sin x · cos x = 1.

Р е ш е н и е . cos ² x + sin x · cos x – sin ² x – cos ² x = 0 ,

sin x · cos x – sin ² x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

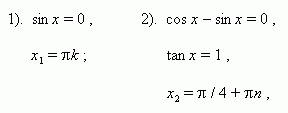
П р и м е р 3. Решить уравнение: cos 2x – cos 8x + cos 6x = 1.

Р е ш е н и е . cos 2x + cos 6x = 1 + cos 8x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

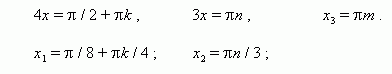
3. Приведение к однородному уравнению. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла. Чтобы решить однородное уравнение, надо: а) перенести все его члены в левую часть; б) вынести все общие множители за скобки; в) приравнять все множители и скобки нулю; г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos ( или sin ) в старшей степени; д) решить полученное алгебраическое уравнение относительно tan . П р и м е р . Решить уравнение: 3sin ² x + 4 sin x · cos x + 5 cos ²x = 2. Р е ш е н и е . 3sin ² x + 4 sin x · cos x + 5 cos ² x = 2sin ² x + 2cos ² x , sin ² x + 4 sin x · cos x + 3 cos ² x = 0 , tan ² x + 4 tan x + 3 = 0 , отсюда y ² + 4y +3 = 0 , корни этого уравнения: y₁ = -1, y₂ = -3, отсюда 1) tan x = –1, 2) tan x = –3,

12 Следующая ⇒