
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА. ТЕОРИЯ ВЕКТОРНОГО ПОЛЯ». Вариант №1. Вариант №2
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
«ТЕОРИЯ ВЕКТОРНОГО ПОЛЯ»
Составители: преподаватели кафедры Вычислительных методов и уравнений математической физики.
Вариант №1
1. Найти производную поля 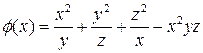 в точке А(1,2,1) в направлении, образующем равные острые углы с осями координат.
в точке А(1,2,1) в направлении, образующем равные острые углы с осями координат.
2. Найти угол между градиентом скалярных полей 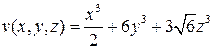 и
и  в точке
в точке 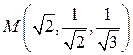 .
.
3. Показать, что поле вектора  потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля градиентов функции 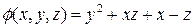 .
.
5. Вычислить работу силы 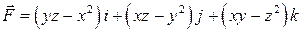 при перемещении по линии
при перемещении по линии 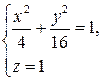 из точки А(2,0,1) в точку В(0,4,1).
из точки А(2,0,1) в точку В(0,4,1).
6. Вычислить поток поля 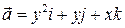 через плоский треугольник с вершинами в точках А(2,0,0), B(0,-1,0), C(2,0,4). Нормальный вектор плоскости образует острый угол с осью Ох.
через плоский треугольник с вершинами в точках А(2,0,0), B(0,-1,0), C(2,0,4). Нормальный вектор плоскости образует острый угол с осью Ох.
7. Найти поток поля 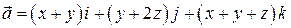 через полусферу
через полусферу 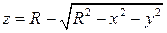 в направлении внешней нормали.
в направлении внешней нормали.
8. Проверить формулу Стокса для вектора  , принимая за поверхность интегрирования боковую поверхность пирамиды, ограниченную плоскостями
, принимая за поверхность интегрирования боковую поверхность пирамиды, ограниченную плоскостями 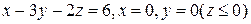 , а за контур интегрирования – линию пересечения её с плоскостью z = 0.
, а за контур интегрирования – линию пересечения её с плоскостью z = 0.
9. Доказать, что 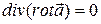 .
.
10. Вычислить 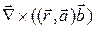 , где
, где 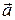 и
и 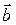 постоянные векторы, а
постоянные векторы, а 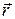 - радиус-вектор точки.
- радиус-вектор точки.
Вариант №2
1. Дано скалярное поля 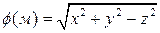 . Найти
. Найти 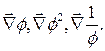 Построить поверхность уровня для
Построить поверхность уровня для 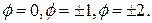
2. Найти производную скалярных полей  в точке
в точке 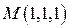 по направлению нормали к поверхности S:
по направлению нормали к поверхности S: 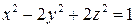 , образующей тупой угол с положительным направлением оси Oz .
, образующей тупой угол с положительным направлением оси Oz .
3. Показать, что поле вектора 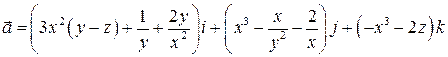 потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля градиентов функции 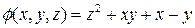 .
.
5. Вычислить работу силы 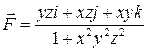 при перемещении по линии (L):
при перемещении по линии (L):  из точки
из точки 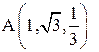 в точку
в точку 
6. Вычислить поток поля 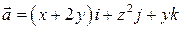 через часть поверхности
через часть поверхности  , лежащую в I октанте и отсеченную плоскостями z = 0, z = 3, в направлении внешней нормали.
, лежащую в I октанте и отсеченную плоскостями z = 0, z = 3, в направлении внешней нормали.
7. Найти поток поля 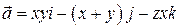 через часть поверхности
через часть поверхности 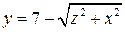 отсеченную плоскостями y = 3 в направлении внешней нормали.
отсеченную плоскостями y = 3 в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора 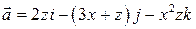 , принимая за поверхность интегрирования – поверхность, лежащей в I октанте образованную поверхностью
, принимая за поверхность интегрирования – поверхность, лежащей в I октанте образованную поверхностью 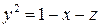 и плоскостями x = 0, z = 0, а за контур интегрирования – линию пересечения этой поверхности с плоскостью
и плоскостями x = 0, z = 0, а за контур интегрирования – линию пересечения этой поверхности с плоскостью
у = 0.
9. Доказать, что вектор 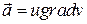 ортогонален к
ортогонален к 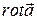 , если
, если 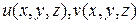 - дифференцируемые скалярные функции.
- дифференцируемые скалярные функции.
10. Найти 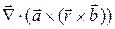 , где
, где 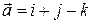 и
и 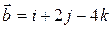 ,
, 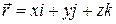 .
.
Вариант №3
1. Найти градиент поля 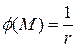 , где
, где 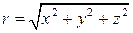 , М(x,y,z). Построить поверхность уровня поля, соответствующие значениям
, М(x,y,z). Построить поверхность уровня поля, соответствующие значениям 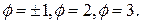
2. Найти производную скалярных полей 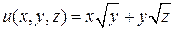 в точке
в точке 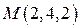 по направлению нормали к поверхности S:
по направлению нормали к поверхности S: 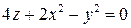 , образующей тупой угол с положительным направлением оси Oz .
, образующей тупой угол с положительным направлением оси Oz .
3. Показать, что поле вектора  потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля градиентов функции 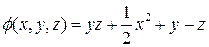 .
.
5. Вычислить работу силы 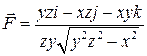 при перемещении по линии от точки
при перемещении по линии от точки 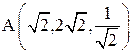 до точку
до точку 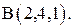
6. Вычислить поток поля  через часть поверхности
через часть поверхности  , лежащую в IV октанте, в направлении внешней нормали.
, лежащую в IV октанте, в направлении внешней нормали.
7. Найти поток поля 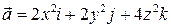 через замкнутую поверхность, образованную полусферой
через замкнутую поверхность, образованную полусферой 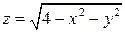 и параболоидом
и параболоидом 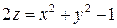 , в направлении внешней нормали.
, в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора 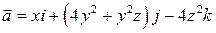 , принимая за контур интегрирования окружность,
, принимая за контур интегрирования окружность, 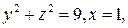 а за поверхность интегрирования – поверхность цилиндра
а за поверхность интегрирования – поверхность цилиндра 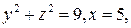 натянутую на этот контур.
натянутую на этот контур.
9. Доказать, что вектор  , где
, где 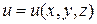 - дифференцируемая функция.
- дифференцируемая функция.
10. Найти 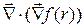 , где
, где 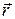 -радиус-вектор точки,
-радиус-вектор точки, 
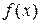 - произвольная дважды дифференцируемая функция. В каком
- произвольная дважды дифференцируемая функция. В каком 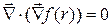 ?
?
Вариант №4
1. Найти вектор напряженности электрического поля, потенциал которого имеет вид 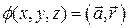 , где
, где 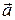 - постоянный вектор,
- постоянный вектор, 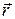 - радиус-вектор точки поля. Построить поверхности равного потенциала для
- радиус-вектор точки поля. Построить поверхности равного потенциала для 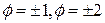 , если
, если 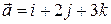 .
.
2. Найти производную скалярных полей  в точке
в точке 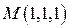 по направлению нормали к поверхности S:
по направлению нормали к поверхности S: 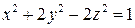 , образующей острый угол с положительным направлением оси Oz .
, образующей острый угол с положительным направлением оси Oz .
3. Показать, что поле вектора 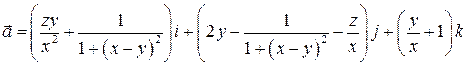 потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля вектора 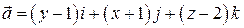 .
.
5. Вычислить работу силы 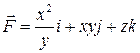 при перемещении по линии (L) от точки
при перемещении по линии (L) от точки 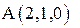 к точке
к точке 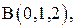 если линия (L) – меньшая дуга кривой
если линия (L) – меньшая дуга кривой 
6. Вычислить поток поля 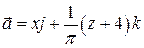 через часть поверхности
через часть поверхности 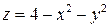 , лежащую в IV октанте, в направлении внешней нормали.
, лежащую в IV октанте, в направлении внешней нормали.
7. Найти поток поля 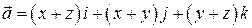 через часть поверхности
через часть поверхности 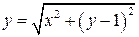 отсеченную плоскостями z =1, в направлении внешней нормали.
отсеченную плоскостями z =1, в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора 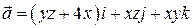 , принимая за поверхность интегрирования эллипс y = 0, а за поверхность интегрирования – часть поверхности цилиндра
, принимая за поверхность интегрирования эллипс y = 0, а за поверхность интегрирования – часть поверхности цилиндра 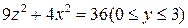 , и
, и 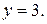
9. Доказать, что 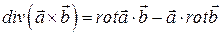 .
.
10. Найти 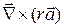 , где
, где  , а
, а  .
.
Вариант №5
1. Потенциал некоторого электростатического поля имеет вид 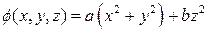 , где “а” и “b” - константы. Найти длину и направление вектора напряженности поля. Какую форму имеют эквипотенциальные поверхности для a > 0, b > 0?
, где “а” и “b” - константы. Найти длину и направление вектора напряженности поля. Какую форму имеют эквипотенциальные поверхности для a > 0, b > 0?
2. Найти производную скалярных полей 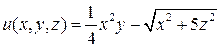 в точке
в точке 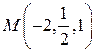 по направлению нормали к поверхности S:
по направлению нормали к поверхности S:  , образующей тупой угол с направлением оси Oz .
, образующей тупой угол с направлением оси Oz .
3. Показать, что поле вектора 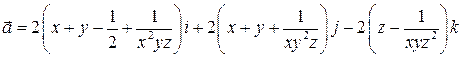 потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля вектора  .
.
5. Вычислить работу вектора силы 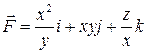 по меньшей дуге окружности
по меньшей дуге окружности 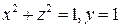 от точки
от точки  до точке
до точке 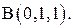
6. Вычислить поток поля 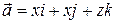 через плоский треугольник с вершинами в точках А(-4,0,0), B(0,2,0), C(-4,0,4). Нормальный вектор плоскости образует с осью Oy острый.
через плоский треугольник с вершинами в точках А(-4,0,0), B(0,2,0), C(-4,0,4). Нормальный вектор плоскости образует с осью Oy острый.
7. Найти поток поля  через границу пространственной области
через границу пространственной области 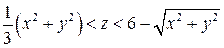 в направлении внешней нормали.
в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора  , принимая за контур интегрирования астроиду
, принимая за контур интегрирования астроиду 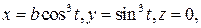 а за поверхность интегрирования – часть плоскости xoy, ограниченную астроидой.
а за поверхность интегрирования – часть плоскости xoy, ограниченную астроидой.
9. Доказать, что поле вектора 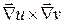 соленоидально, если
соленоидально, если  ,
, 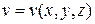 - дифференцируемые скалярные функции.
- дифференцируемые скалярные функции.
10. Найти 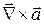 , где
, где 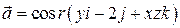 ,
,  -радиус-вектор точки,
-радиус-вектор точки, 
Вариант №6
1. Потенциал некоторого электростатического поля имеет вид 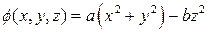 , где “а” и “b” - константы. Найти модуль и направление вектора напряженности поля. Какую форму имеют эквипотенциальные поверхности в случае a > 0, b > 0?
, где “а” и “b” - константы. Найти модуль и направление вектора напряженности поля. Какую форму имеют эквипотенциальные поверхности в случае a > 0, b > 0?
2. Найти производную скалярных полей 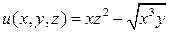 в точке
в точке 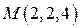 по направлению нормали к поверхности S:
по направлению нормали к поверхности S: 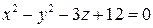 , образующей острый угол с положительным направлением оси Oz .
, образующей острый угол с положительным направлением оси Oz .
3. Показать, что поле вектора 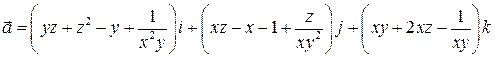 потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля вектора 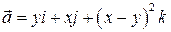 .
.
5. Вычислить работу вектора силы 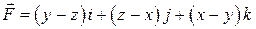 при перемещении по линии
при перемещении по линии 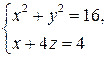 .
.
6. Вычислить поток поля 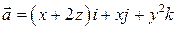 через часть поверхности
через часть поверхности 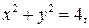 лежащую в II октанте и отсеченную плоскостями z = 0, z = 1 в направлении внешней нормали.
лежащую в II октанте и отсеченную плоскостями z = 0, z = 1 в направлении внешней нормали.
7. Найти поток поля 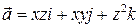 через часть поверхности
через часть поверхности 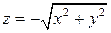 , отсеченную плоскостью z = -2, в направлении внешней нормали.
, отсеченную плоскостью z = -2, в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора 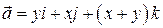 , принимая за поверхность интегрирования – поверхность, лежащую в первом октанте, образованную параболоидом
, принимая за поверхность интегрирования – поверхность, лежащую в первом октанте, образованную параболоидом 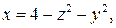 а за контур интегрирования – линию пересечения этой поверхности с плоскостью x = 0.
а за контур интегрирования – линию пересечения этой поверхности с плоскостью x = 0.
9. Доказать, что 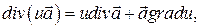 где
где  - дифференциальная функция.
- дифференциальная функция.
10. Найти 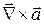 и
и 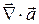 , для поля вектора
, для поля вектора 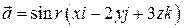 , где
, где 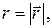
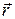 - радиус-вектор точки.
- радиус-вектор точки.
Вариант №7
1. Потенциальная энергия части имеет вид 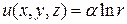 , где
, где 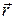 - модуль радиуса - вектора
- модуль радиуса - вектора 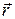 частицы,
частицы, 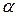 - постоянная величина. Найти силу
- постоянная величина. Найти силу 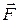 действующую на частицу. Какую форму имеют поверхности, для которой модуль вектора силы
действующую на частицу. Какую форму имеют поверхности, для которой модуль вектора силы 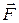 постоянен? Изобразить эти поверхности для случаев
постоянен? Изобразить эти поверхности для случаев 
2. Найти производную скалярных полей 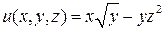 в точке
в точке 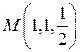 по направлению нормали к поверхности S:
по направлению нормали к поверхности S: 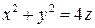 , образующей острый угол с положительным направлением оси Oz .
, образующей острый угол с положительным направлением оси Oz .
3. Показать, что поле вектора  потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля вектора 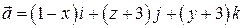 .
.
5. Вычислить циркуляцию вектора 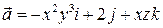 вдоль контура
вдоль контура 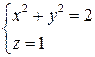 .
.
6. Вычислить поток поля 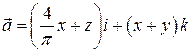 через часть поверхности
через часть поверхности  , лежащую в I октанте, в направлении внешней нормали.
, лежащую в I октанте, в направлении внешней нормали.
7. Найти поток поля  через границу выпуклой области, заключенной между поверхностями
через границу выпуклой области, заключенной между поверхностями 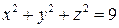 и
и 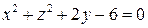 , в направлении внешней нормали.
, в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора  , принимая за контур интегрирования окружность
, принимая за контур интегрирования окружность 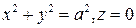 , а за поверхность интегрирования – поверхность цилиндра
, а за поверхность интегрирования – поверхность цилиндра  и
и 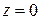 .
.
9. Доказать, что 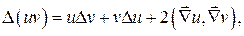 если
если  ,
, 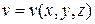 - дважды дифференцируемые скалярные функции.
- дважды дифференцируемые скалярные функции.
10. Найти 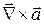 и
и 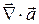 , для поля вектора
, для поля вектора  , где
, где 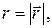
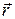 - радиус-вектор точки.
- радиус-вектор точки.
Вариант №8
1. Потенциал энергия частицы имеет вид 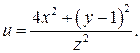 Найти силу
Найти силу 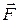 , действующую на частицу. Построить эквипотенциальные поверхности в случае u = 0, u = 1, u = 4.
, действующую на частицу. Построить эквипотенциальные поверхности в случае u = 0, u = 1, u = 4.
2. Найти производную функции  в точке
в точке 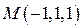 в направлению градиента функции
в направлению градиента функции 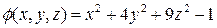 .
.
3. Показать, что поле вектора 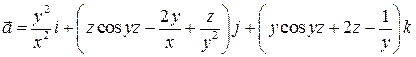 потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля вектора 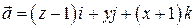 .
.
5. Вычислить работу вектора силы 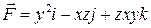 при перемещении по меньшей дуге кривой
при перемещении по меньшей дуге кривой 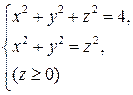 от точки
от точки 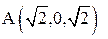 к точке
к точке 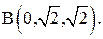 .
.
6. Вычислить поток поля 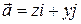 через часть поверхности
через часть поверхности 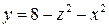 , лежащую в II октанте, в направлении внешней нормали.
, лежащую в II октанте, в направлении внешней нормали.
7. Найти поток поля 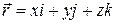 через часть поверхности
через часть поверхности 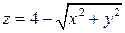 , отсеченную плоскостью z = 2, в направлении внешней нормали.
, отсеченную плоскостью z = 2, в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора 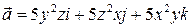 , принимая за контур интегрирования часть параболы
, принимая за контур интегрирования часть параболы 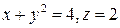 и замыкающей её прямой z = 2, x = 0, а за поверхность интегрирования часть поверхности z = 2, ограниченную этим контуром.
и замыкающей её прямой z = 2, x = 0, а за поверхность интегрирования часть поверхности z = 2, ограниченную этим контуром.
9. Доказать, что 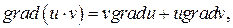 где
где 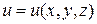 ,
, 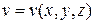 - дифференцируемые функции. Проверить, что
- дифференцируемые функции. Проверить, что 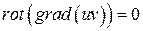 .
.
10. Для поля вектора 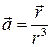 найти потенциал,
найти потенциал, 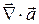 ,
, 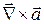 и векторные линии, если
и векторные линии, если 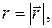
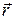 - радиус-вектор точки.
- радиус-вектор точки.
Вариант №9
1. Потенциал энергия частицы имеет вид 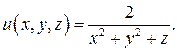 Найти силу
Найти силу 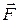 , действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае
, действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае 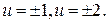
2. Найти производную скалярного поля 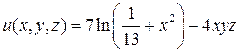 в точке
в точке 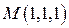 по направлению нормали к поверхности
по направлению нормали к поверхности 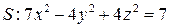 , образующей тупой угол с положительным направлением оси Oz .
, образующей тупой угол с положительным направлением оси Oz .
3. Показать, что поле вектора 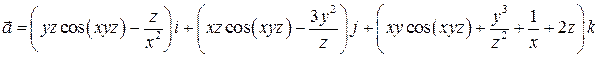 потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля вектора 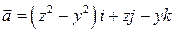 .
.
5. Вычислить работу вектора силы 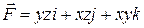 при перемещении по кривой
при перемещении по кривой 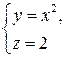 от точки
от точки 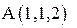 к точке
к точке 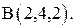
6. Вычислить поток поля 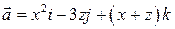 через плоский четырех с вершинами в точках М1(1,-2,4), М2(3,2,4), М3(-1,2,4), М4(-3,-2,4) в направлении оси Oz.
через плоский четырех с вершинами в точках М1(1,-2,4), М2(3,2,4), М3(-1,2,4), М4(-3,-2,4) в направлении оси Oz.
7. Найти поток поля 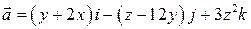 через замкнутую поверхность, ограничивающую пространственную область
через замкнутую поверхность, ограничивающую пространственную область 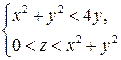 , в направлении внешней нормали.
, в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора 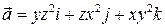 , принимая за контур интегрирования окружность
, принимая за контур интегрирования окружность 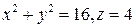 , а за поверхность интегрирования – любую поверхность, натянутую на эту окружность.
, а за поверхность интегрирования – любую поверхность, натянутую на эту окружность.
9. Доказать, что 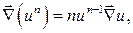 где
где 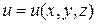 - дифференцируемая функция.
- дифференцируемая функция.
10. Найти 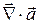 и
и 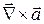 для вектора
для вектора  где
где 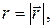
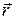 - радиус-вектор точки.
- радиус-вектор точки.
Вариант №10
1. Потенциал энергия частицы имеет вид 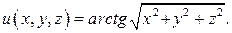 Найти силу
Найти силу 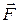 , действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае
, действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае 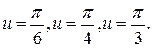
2. Найти производную скалярного поля 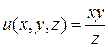 по направлению вектора
по направлению вектора 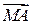 в точке М, если
в точке М, если 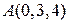
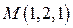 .
.
3. Показать, что поле вектора 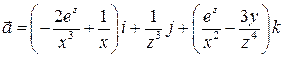 потенциально, найти потенциал поля.
потенциально, найти потенциал поля.
4. Найти векторные линии поля вектора 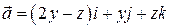 .
.
5. Вычислить работу силы 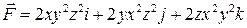 при перемещении по прямой из точки
при перемещении по прямой из точки 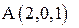 к точке
к точке 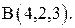
6. Вычислить поток поля  через часть поверхности
через часть поверхности 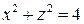 , лежащую в I октанте и отсеченную плоскостями y = 1, y = 4, в направлении внешней нормали.
, лежащую в I октанте и отсеченную плоскостями y = 1, y = 4, в направлении внешней нормали.
7. Найти поток поля 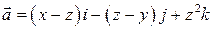 через замкнутую поверхность, ограничивающую область
через замкнутую поверхность, ограничивающую область 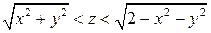 , в направлении внешней нормали.
, в направлении внешней нормали.
8. Проверить формулу Стокса для поля вектора 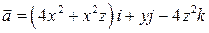 , принимая за контур интегрирования окружность
, принимая за контур интегрирования окружность 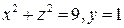 , а за поверхность интегрирования – полусферу, натянутую на этот контур.
, а за поверхность интегрирования – полусферу, натянутую на этот контур.
9. Вычислить 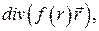 где
где 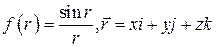 . Доказать, что пространственное поле вектора
. Доказать, что пространственное поле вектора 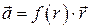 будет соленоидальным только тогда, когда
будет соленоидальным только тогда, когда 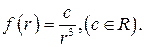
10. Найти  , где
, где 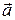 - постоянный вектор,
- постоянный вектор, 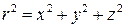 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|