
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Прямоугольный треугольник. Вычисление сторон и углов.(С тригонометрией) Задание В6.
Для решения задач на нахождение сторон и углов прямоугольного треугольника нужно вспомнить определения синуса, косинуса и тангенса.
Рассмотрим прямоугольный треугольник:
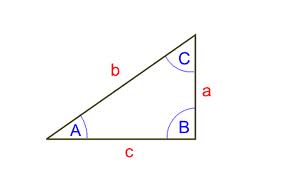 Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Противолежащий катет – это тот катет, который лежит напротив угла, синус которого мы рассматриваем.
Например, для треугольника, который изображен на рисунке, 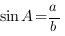 ,
, 
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Прилежащий катет – это тот катет, который является одной из сторон угла, косинус которого мы рассматриваем.
Например, для треугольника, который изображен на рисунке, 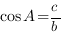 ,
, 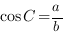
Тангенсом острого угла прямоугольного теругольника называется отношение противолежащего катета к прилежащему.
Например, для треугольника, который изображен на рисунке, 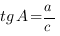 ,
, 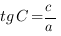
Задачи на нахождение сторон и углов прямоугольного треугольника решаются по такому алгоритму:
1. Выделяем треугольник, в который входит сторона или угол, который нам нужно найти.
2. Смотрим, какие элементы треугольника нам известны, и с помощью какой тригонометрической функции они между собой связаны.
3. Записываем соотношение, которое связывает между собой эти элементы,
Рассмотрим примеры решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике.
1. Задание В6 (№ 27217) В треугольнике 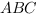 угол
угол 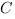 равен
равен 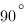 ,
, 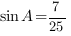 . Найдите
. Найдите 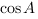
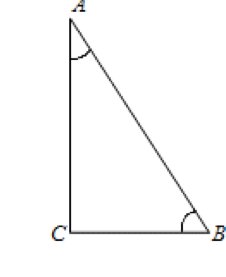
рис.1
Решим эту задачу двумя способвми.
а. Так как требуется найти косинус угла, синус которого известен, мы можем воспользоваться основным тригонометрическим тождеством.
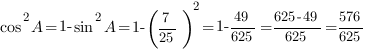
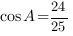
б. 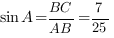
Введем единичный отрезок 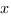 , тогда
, тогда 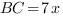 ,
, 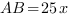
По теореме Пифагора 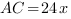 .
.
Тогда 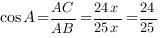
Ответ: 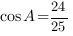
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|