
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры решения задач по векторной алгебре
. Примеры решения задач по векторной алгебре
Пример 1. Найти длину вектора 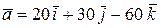 и его направляющие косинусы.
и его направляющие косинусы.
Решение:
½ 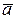 ½=
½= 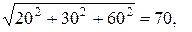
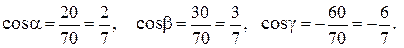
Пример 2.Найти скалярное произведение векторов 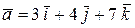 ,
, 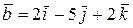 .
.
Решение: Находим 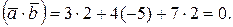 Так как
Так как 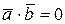 и
и 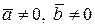 , то
, то 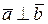 .
.
Пример 3.Определить, при каком значении m векторы 3 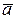 + m
+ m 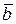 и
и 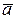 – 2
– 2 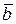 будут взаимно перпендикулярны, если ½
будут взаимно перпендикулярны, если ½ 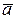 ½= 7
½= 7 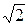 ; ½
; ½ 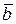 ½= 4; (
½= 4; ( 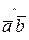 ) =
) = 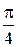 .
.
Решение:
Если два вектора взаимно перпендикулярны, то их скалярное произведение равно нулю.
Возьмем скалярное произведение векторов 3 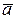 + m
+ m 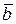 и
и 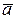 – 2
– 2 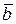 и, приравняв его нулю, найдем m:
и, приравняв его нулю, найдем m:
(3 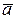 + m
+ m 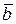 )(
)( 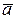 – 2
– 2 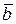 ) = 0;
) = 0;
3 ½ 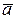 ½2– 6 ½
½2– 6 ½ 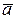 ½½
½½ 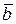 ½cos
½cos 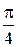 + m½
+ m½ 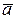 ½½
½½ 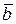 ½cos
½cos 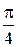 – 2 m½
– 2 m½ 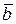 ½2 = 0;
½2 = 0;
3 × 49 × 2 – 6 × 7 × 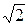 × 4
× 4 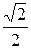 + m × 7
+ m × 7 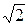 × 4
× 4 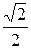 – 2 × m × 16 = 0;
– 2 × m × 16 = 0;
294 – 168 + 28 m – 32 m = 0, 4 m =126, m = 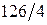 = 31,5.
= 31,5.
Пример 4.Определить угол между векторами 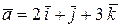 и
и 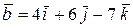 .
.
Решение:
Так как 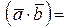 ½
½ 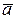 ½½
½½ 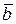 ½cosj , то cosj =
½cosj , то cosj = 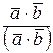 . Имеем
. Имеем
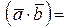 2 × 4 + 1 × 6 – 3 × 7 = –7;
2 × 4 + 1 × 6 – 3 × 7 = –7;
½ 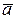 ½=
½= 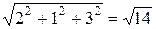 ; ½
; ½ 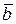 ½=
½= 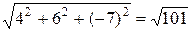 .
.
Следовательно,
cos j = 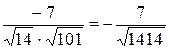 , j = arccos
, j = arccos 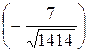 .
.
Пример 5.Найти векторное произведение векторов 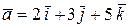 и
и 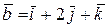 .
.
Решение:
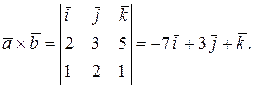
Пример 6.Вычислить площадь параллелограмма, построенного на векторах 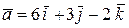 и
и 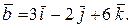
Решение:
Находим векторное произведение 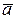 на
на 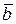 :
:
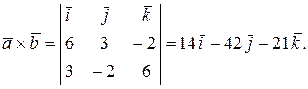
Так как модуль векторного произведения двух векторов равен площади построенного на них параллелограмма, то S =½ 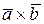 ½=
½= 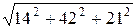 = 49 (кв. ед.).
= 49 (кв. ед.).
Пример 7. Найти площадь треугольника ABC с вершинами A (1, 2, 0), B (3, 0, –3) и C (5, 2, 6).
Решение:
Площадь треугольника ABC равна половине площади параллелограмма, построенного на векторах 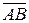 и
и 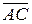 : SD =
: SD = 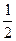 ½
½ 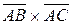 ½. Найдем векторы
½. Найдем векторы 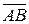 и
и 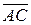 :
: 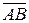 =
= 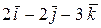 ;
; 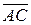 =
= 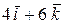 .
.
Их векторное произведение
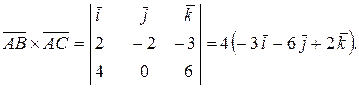 ,
,
поэтому ½ 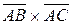 ½ = 4 ½
½ = 4 ½ 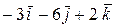 ½= 4
½= 4 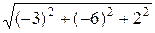 = 28, и следовательно, SD = 14 (кв. ед.)
= 28, и следовательно, SD = 14 (кв. ед.)
Пример 8. Вычислить площадь параллелограмма, построенного на векторах 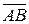 = 6
= 6 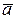 – 3
– 3 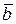 и
и 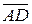 = 3
= 3 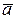 + 2
+ 2 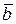 , если ½
, если ½ 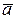 ½= 3; ½
½= 3; ½ 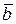 ½= 5; (
½= 5; ( 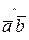 )=
)= 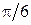 .
.
Решение:
Имеем 18 ( 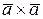 ) –9 (
) –9 ( 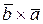 ) +12 (
) +12 ( 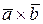 ) – 6 (
) – 6 ( 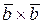 ) = 21(
) = 21( 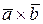 ), где
), где
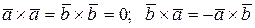 .
.
Итак, S =½ 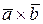 ½= 21 ×3 × 5 ×
½= 21 ×3 × 5 × 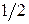 = 157,5 (кв. ед.)
= 157,5 (кв. ед.)
Пример 9.Найти смешанноепроизведение векторов 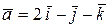 ,
, 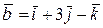 и
и 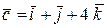 .
.
Решение:
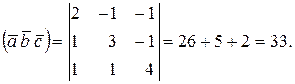
Пример 10.Показать, что векторы 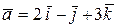 ,
, 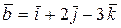 и
и 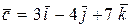 компланарны.
компланарны.
Решение:
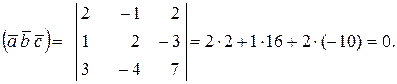
Так как 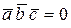 , то заданные векторы компланарны.
, то заданные векторы компланарны.
Пример 11.Найти объем треугольной пирамиды с вершинами A (2, 2, 2), B (4, 3, 3), C (4, 5, 4) и D (5, 5, 6).
Решение:
Найдем векторы 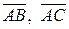 и
и 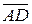 , совпадающие с ребрами пирамиды, сходящимися в вершине A:
, совпадающие с ребрами пирамиды, сходящимися в вершине A: 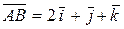 ,
, 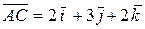 ,
, 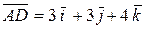 .
.
Находим смешанное произведение этих векторов:
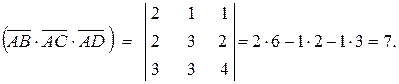
Так как объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах 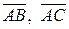 и
и 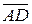 , то Vпир =
, то Vпир = 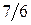 (куб. ед.).
(куб. ед.).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|