Нелинейные искажения

Основы электрики

Амплитудно-частотная характеристика (АЧХ) — функция, показывающая зависимость модуля некоторой комплекснозначной функции от частоты. Также может рассматриваться АЧХ других комплекснозначных функций частоты, например, спектральной плотности мощности сигнала.

АЧХ в теории линейных стационарных систем означает зависимость модуля передаточной функции системы от частоты. АЧХ показывает во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на всём диапазоне частот.

Фазо-частотная характеристика (ФЧХ) — частотная зависимость разности фаз между выходным и входным сигналами.

Часто ФЧХ используют для оценки фазовых искажений формы сложного сигнала, вызываемых неодинаковой задержкой во времени его отдельных гармонических составляющих при их прохождении по цепи

§ В теории управления ФЧХ звена определяется из равенства её тангенса отношению мнимой части АФЧХ к действительной:

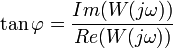
Нелинейные искажения

Нелинейными искажениями принято считать изменения сигнала, приводящие к появлению новых спектральных составляющих. Строго говоря, обсуждение этого феномена имеет смысл при условии, что спектр сигнала конечен, а это достигается только для бесконечных во времени сигналов. С достаточной для практики точностью это ограничение в звукотехнике обходится, но забывать про него нельзя.

К появлению новых спектральных составляющих приводит нелинейность амплитудной характеристики цепи, именно отсюда и пришло название. Мерой нелинейности принято считать в аудиотехнике соотношение мощностей гармоник и основного тона.

Для измерения напряжения высших гармоник в большинстве аналоговых приборов используется режекторный фильтр, подавляющий основной тон. Сам основной тон не выделяется, а измеряется весь выходной сигнал испытуемого устройства, прибор показывает значение, которое практически совпадает с коэффициентом гармоник.

При полигармоническом воздействии на выходе появляются еще и интермодуляционные составляющие. Если амплитудная характеристика устройства имеет вид Y(X) = X², то в спектре появятся вторые гармоники первого (2F₁) и второго (2F₂) сигналов, а также интермодуляционные составляющие — разность (F₁ — F₂) и сумма (F₁ + F₂) их частот и постоянная составляющая.

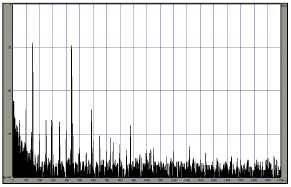
Рис.1. Спектр акустического сигнала, на входе АС двухтональный сигнал: 150 и 440 Гц

Если нелинейность тракта имеет более высокий порядок, то, подав на вход два синусоидальных сигнала с частотами F₁ и F₂ в спектре выходного сигнала, мы обнаружим много составляющих (рис.1).

12 3 Следующая ⇒