Определение производной. Написать конспект, выполнить задания в конце файла. По вариантам: у нечетных номеров - 1 вариант, у четных – 2 вариант. СДАТЬ ДО 09.04. Алгоритм нахождения производной для функции.

Определение производной

Написать конспект, выполнить задания в конце файла. По вариантам: у нечетных номеров - 1 вариант, у четных – 2 вариант. СДАТЬ ДО 09.04

Определение 1.

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁-x₀ называют приращением аргумента, а разность f(x₁)-f(x₀) называют приращением функции.

Приращение аргумента - ∆x. Приращение функции - ∆f или ∆y.

Пример 1.

Найдите приращение функции y=x² при переходе от точки x₀= 1 к точке: а) x₁=1.2; б) x₁=0,96.

Решение.

а) f(x)=x², тогда f(1)=1²=1, а f(1,2)=1,2²=1,44. Отсюда ∆y=∆f=f(1,2)-f(1)=1,44-1=0,44

б) ) f(x)=x², тогда f(1)=1²=1, а f(0,96)= 0,96²=0,9216. Отсюда ∆y=∆f=f(0,96)-f(1)=-0,0784.

Определение2.

Если функция y=f(x) имеет производную в точке x, то её называют дифференцируемой в точкеx.

Процедуру нахождения производной функции y=f(x) называют дифференцированием функции.

Определение 3.

Если функция дифференцируема в точке, то она и непрерывна в этой точке.

Алгоритм нахождения производной для функции.

1.зафиксировать значение x, найти f(x).

2. Дать аргументу x приращение ∆x. Найти значение функции в точке x+∆x, т.е. f(x+∆x).

3. Найти приращение функции: y=f(x+∆x)-f(x).

4. Составить соотношение .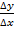

5. Вычислить 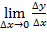. Этот предел и есть производная функции y=f(x).

Для основных простейших функций существуют формулы для нахождения производных, которые находились с помощью рассмотренного нами алгоритма. Была замечена закономерность и эта закономерность между одного вида функциями была систематизирована. Мы будем пользоваться готовым формулами для нахождения производных простейших функций.

При объяснении нового материала используется презентация «Производная» и (или) опорные конспекты с таблицами.

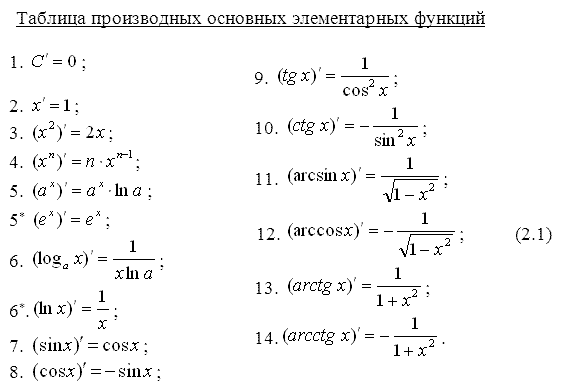
Задания для самостоятельной работы:

Вариант 1	Вариант 2
Найдите производную функции
f(x) = x⁸ f(x) = -4x³ f(x) = 3x⁷ – 6x⁵ – 4x² + 17 f(x) = 3lnx f(x) = sinx+4 tgx f(x) = 6arctgx -arcctgx	f(x) = x¹⁰ f(x) = -6x² f(x) = 6х⁵ – 4х⁴ – 3х + 27 f(x) =7 lnx f(x) = cosx- 2 ctgx f(x) = arccosx+ 8arcsinx
Вычислите значение производной данной функции в данной функции в точке х₀
f(x) = х⁴ – 2х³ + х, х₀= - 1	f(x) = х⁵ – 3х⁴ + х, х₀= - 2
Решите неравенство f ′(x) < 0
f(x) = 2x³ + 12x²	f(x) = 12x³ + 2x⁴
Вычислите f ′(x) = 0
f (x) = 9х² + 72х	f (x) = 6х² + 32х + 2008