Аксиоматическое построение теории вероятностей

Геометрические вероятности

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).

Приведем формальное определение вероятностей для испытаний с бесконечным числом исходов. В подобных случаях пространство элементарных исходов может быть областью 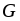, а под событием 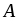можно понимать исходы, входящие в область .

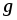Пусть на область 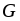наугад бросается «точка». Какова вероятность того, что эта точка попадет в область 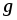, являющуюся частью области ?

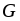1.Пусть отрезок 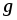, длину которого обозначим как 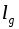, составляет часть отрезка 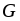длина которого 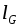. На отрезок 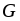наудачу поставлена точка. Это означает выполнение следующих предположений:

поставленная точка может оказаться в любой точке отрезка ;
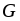вероятность попадания точки на отрезок 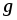пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка .

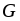В этих предположениях вероятность попадания точки на отрезок 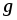определяется равенством .

2.Пусть плоская фигура 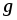с площадью 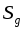составляет часть плоской фигуры 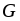, площадь которой 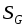. На фигуру 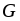наудачу брошена точка. Это означает выполнение следующих предположений:

брошенная точка может оказаться в любой точке фигуры ;
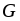вероятность попадания брошенной точки на фигуру 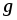пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно фигуры 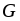, ни от формы .

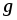В этих предположениях вероятность попадания точки на фигуру 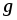определяется равенством .

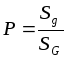3.Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область 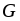объема 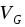, содержащую область 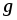объема : .

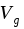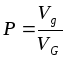В общем случае понятие геометрической вероятности вводится следующим образом.

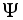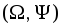Пусть – некоторое множество (базис), а –s-алгебра его подмножеств. Функция называется мерой, на , если она удовлетворяет условиям:

Для любого множества 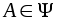его мера неотрицательна: ;
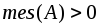Для любого счетного набора попарно непересекающихся множеств 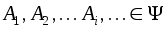мера их суммы равна сумме их мер: 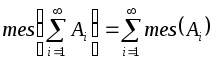– свойство счетной аддитивности.

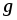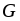Обозначим меру области (длину, площадь, объем) через , а меру области – через ; обозначим через 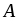событие «попадание брошенной точки в область 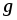, которая содержится в области 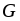_». Вероятность события 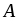, т.е. вероятность попадания в область 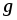точки, брошенной в область 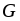, определяется формулой:

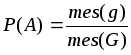Аксиоматическое построение теории вероятностей

Наиболее распространенной в настоящее время является логическая схема построения основ теории вероятностей, которая была разработана А.Н.Колмогоровым в 1933 году.

Основные черты этой схемы следующие.

При изучении какой-либо задачи методами теории вероятностей, прежде всего, выделяется множество 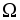, называемое пространством элементарных исходов. Элементы этого множества составляют совокупность возможных исходов наблюдения –элементарных событий. Всякое случайное событие описывается совокупностью благоприятствующих ему элементарных исходов и, поэтому, рассматривается как множество элементарных событий. Некоторые из этих случайных событий образуют борелево множество 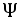наблюдаемых событий 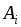, каждому из которых сопоставлено некоторое определенное число 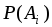, т.е. на 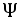заданафункция множеств.

Поскольку каждое наблюдение должно иметь, по крайней мере, хотя бы один исход, все пространство элементарных событий 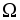соответствует достоверному событию, а пустое множество 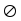– невозможному событию. С событиями 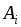изs–алгебры 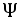связываются определенные числа 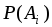, называемые их вероятностями и удовлетворяющие следующему определению.

Вероятностью называется функция множеств, заданная на s–алгебре 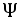пространства элементарных исходов 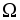и удовлетворяющая следующим условиям:

1. ;

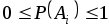2. , т.е. вероятность достоверного события равна единице;

3. Вероятность события 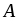, заключающееся в том, что наступит одно из попарно несовместных событий 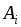( 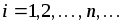), составляет

.

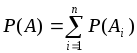Эти условия должны выполняться и для бесконечных последовательностей попарно несовместных событий, т.е. должны выполняться также и условия в определении s–алгебры 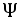. Таким образом, из условия 3 следует:

.

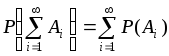Эти условия составляют аксиомы теории вероятностей.

Вся теория вероятностей строится на этих трех аксиомах. Исходные аксиомы постулируются и попытка доказать их лишена смысла. Единственным возможным критерием справедливости этих аксиом является степень, с которой теория, построенная на их основе, отражает реальность. Этот критерий, кстати, справедлив и для любой другой естественнонаучной теории.

Итак, определенная теоретико–вероятностная схема задается тремя компонентами 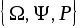, т.е.:

· конкретным пространством элементарных исходов 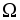, выступающим в роли базиса, в котором описываются все наблюдаемые события;

· конкретным набором подмножеств 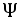пространства элементарных исходов 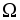, образующимs–алгебру и являющимся областью определения функции вероятности ;

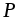· конкретным заданием вероятностей 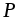на всех множествахs–алгебры .

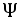Набор этих трех компонент 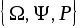, удовлетворяющий аксиомам теории вероятностей, называетсявероятностным пространствомиливероятностной схемой.