
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема урока: ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА.
Тема урока: ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА.
Синус, косинус и тангенс половинного угла.
Цели урока: на основе полученных ранее знаний, вывести формулы для вычисления sin2x, cos2x, tg2x, показать их применение, развить умение использовать эти формулы в тригонометрических преобразованиях.
Ход урока:
1. Проверка домашнего задания (№482(2,4), №485(2,3)).
2. Повторение (Вспомним формулу синус суммы, косинус суммы и тангенс суммы аргументов).
1. 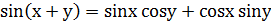
2. 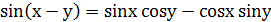
3. 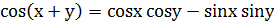
4. 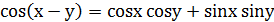
5. 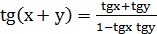
6. 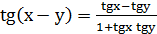
Давайте, пользуясь формулами, которые мы только что вспомнили, выведем следующее формулы.
3. Изучение нового материала.
Вывод формул двойного аргумента:
1. Из формулы косинуса суммы двух аргументов, заменив β на α, получить формулу косинуса двойного аргумента.
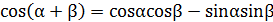
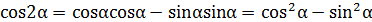
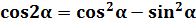
2. Из формулы синуса суммы двух аргументов, заменив β на α, получить формулу синуса двойного аргумента.
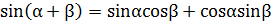
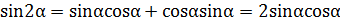
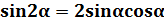
3. Из формулы тангенса суммы двух аргументов, заменив β на α, получить формулу тангенса двойного аргумента.
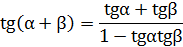
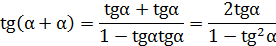
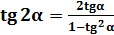 .
.
4. Закрепление изученного материала.
Показать применение данных формул.
1.Упростить выражение:
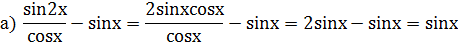
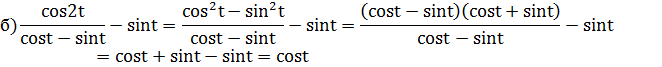
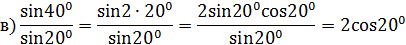
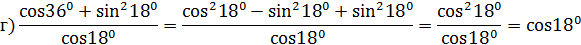
А теперь докажем два тождества, используя доказанную в начале урока формулу cos 2x = cos 2x – sin2x
1. Доказать тождество:
cos2x = 1 – 2sin2x
Зная, что 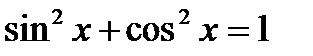 , получаем:
, получаем:
cos2x = cos2x – sin2x = (1 - sin2x) - sin2x = 1 - 2 sin2x
cos2x = 1 - 2 sin2x
2. Доказать тождество:
cos2x = 2cos2x – 1
cos2x = cos2x – sin2x = cos2x – (1 - cos2x) = 2cos2x – 1
cos2x = 2cos2x – 1
3. Выразить sin2x из равенства:
cos2x = 1 - 2sin2x
2 sin2x = 1 – cos2x
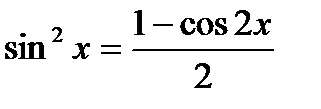
4. Выразить cos2x из равенства:
cos2x = 2cos2x – 1
cos2x+1 = 2cos2x
2cos2x = cos2x+1
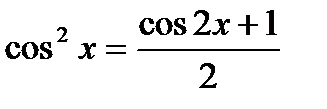
Итак, выполняя №1 и №2, мы получили еще два варианта формулы двойного аргумента, а выполняя №3 и №4, вывели формулы понижения степени.
Связь тригонометрических функций с тангенсом половинного аргумента
В ряде случаев полезны следующие формулы:
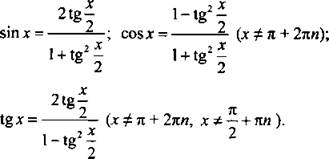
5. Выполнить самостоятельно в тетрадях с последующей проверкой.
№501, №502, №506 (3,4)
Домашнее задание. 1) Конспект занятия.
2) Выучить формулы:
1. Формулы двойного аргумента.
2. Формулы тройного аргумента.
3. Связь тригонометрических функций с тангенсом половинного аргумента.
3) Выполнить номера №501, №502, №506 (3,4).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|