ПРИМЕР (решение задач кинематики точки)

ПРИМЕР (решение задач кинематики точки)

По дуге радиуса R , равномерно-замедленно двигается точка, ее скорость в начальном движении по дуге составила V₀ =15 м/с. После того, как точка прошла расстояние S = 500 м, ее скорость уменьшилась до V =10 м/с. Определить полное ускорение в начале и конце движения.

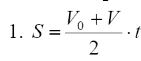Отсюда определим время t:

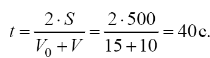
2. Определим касательное ускорение a_τ:

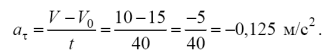
a_τ = const в течение всего времени движения.

3. Найдем нормальное ускорение: в начале движения оно равно

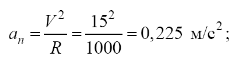
в конце пути –

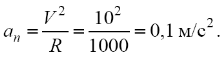
4. Величины полных ускорений равны:

в начале движения

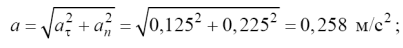
в конце пути

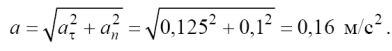
ПРИМЕР (решение задач кинематики вращательного движения твердого тела)

Задачи кинематики поступательного движения твердого тела сводятся к решению задач кинематики точки.

Определить, за какое время тело достигнет угловой скорости 70 рад/с, если оно движется согласно уравнения φ = 5t + 1,2t³. Сколько оборотов за это время успеет совершить тело и какой величины достигнет угловое ускорение.

РЕШЕНИЕ

Угловая скорость характеризует быстроту изменения угла поворота φ тела с течением времени t.

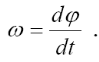Согласно данным задачи

ω = 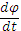= 5 + 3.6 t²

тогда угловая скорость ω достигнет значения 70 рад/с в момент времени t= 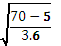= 4.25 c. Зная время, определим угол поворота 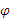за 4,25 с.

φ = 5 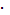4,25 + 1,2 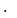4,25³=113,37 рад.

Учитывая, что один оборот N равен 2 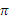рад угол поворота φ, т.е. 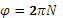, отсюда N= 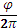= 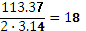,05 оборотов.