
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 1 № 514051. Решение.. Задание 2 № 511686. Решение.. Задание 3 № 81287. Решение.. Задание 4 № 509649. Решение.. Задание 5 № 507996. Решение.. Задание 6 № 24429. Решение.. Задание 7 № 500887. Решение.. Задание 8 № 508040. Решение.. Задание 9 № 51000
1. Задание 1 № 514051
Найдите значение выражения 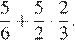
Решение.
Найдем значение выражения:
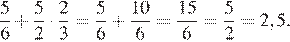
Ответ: 2,5.
2. Задание 2 № 511686
Найдите значение выражения 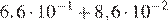 .
.
Решение.
Найдём значение выражения:
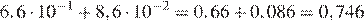
Ответ: 0,746.
3. Задание 3 № 81287
Только 57% из 23 000 выпускников города правильно решили задачу B9. Сколько человек правильно решили задачу B9?
Решение.
Правильно решили задачу 23 000  0,57 = 13 110 учеников.
0,57 = 13 110 учеников.
Ответ: 13 110.
4. Задание 4 № 509649
Длина биссектрисы lc, проведённой к стороне c треугольника со сторонами a, b и c, вычисляется по формуле 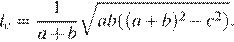 Найдите длину биссектрисы lc, если a = 3, b = 9,
Найдите длину биссектрисы lc, если a = 3, b = 9, 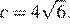
Решение.
Найдём длину биссиктрисы:
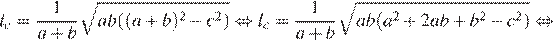
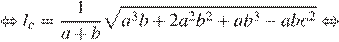

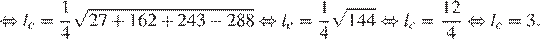
Ответ: 3.
5. Задание 5 № 507996
Найдите значение выражения 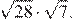
Решение.
Найдём значение выражения:
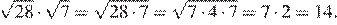
Ответ: 14.
6. Задание 6 № 24429
В летнем лагере на каждого участника полагается 30 г сахара в день. В лагере 148 человек. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 5 дней?
Решение.
На 148 человек на 1 день полагается 148  30 = 4440 г сахара, на 5 дней — 4440
30 = 4440 г сахара, на 5 дней — 4440  5 = 22 200 г. Разделим 22 200 на 1000:
5 = 22 200 г. Разделим 22 200 на 1000:
22 200 : 1000 = 22,2.
Значит, на весь лагерь на 5 дней понадобится 23 килограммовых упаковки сахара.
Ответ: 23.
7. Задание 7 № 500887
Найдите корень уравнения 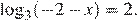
Решение.
Пользуясь определением логарифма, имеем:

Ответ:−11.
8. Задание 8 № 508040
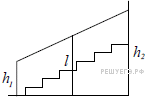 Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 1,65 м, а наибольшая h2 равна 2,65 м. Ответ дайте в метрах.
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 1,65 м, а наибольшая h2 равна 2,65 м. Ответ дайте в метрах.
Решение.
Заметим, что данная конструкция представляет собой трапецию, а столб — средняя линия данной трапеции. Длина средней линии трапеции равна полусумме оснований:
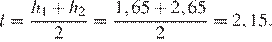
Ответ: 2,15.
9. Задание 9 № 510005
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ | |
| А) масса двухлитрового пакета сока Б) масса взрослого кита В) масса косточки персика Г) масса таблетки лекарства | 1) 130 т 2) 2 кг 3) 400 мг 4) 8 г |
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В | Г |
Решение.
От легкого к тяжелому: масса таблетки лекарства (Г - 3), масса косточки персика (В - 4), масса двухлитрового пакета сока (А - 2) и масса взрослого кита (Б-1). Окончательно получим 2143.
Ответ: 2143.
10. Задание 10 № 283577
В чемпионате по гимнастике участвуют 50 спортсменок: 22 из Великобритании, 19 из Франции, остальные — из Германии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Германии.
Решение.
В чемпионате принимает участие 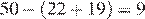 спортсменок из Германии. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Германии, равна
спортсменок из Германии. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Германии, равна
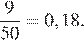
Ответ: 0,18.
11. Задание 11 № 510917
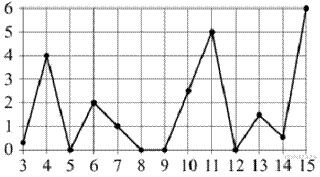
На рисунке жирными точками показано суточное количество осадков, выпавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линиями. Определите по рисунку, какого числа выпало наибольшее количество осадков за данный период.
Решение.
Из графика видно, что наибольшее число осадков выпало 15 февраля.
Ответ: 15
12. Задание 12 № 18499
Для транспортировки 3 тонн груза на 250 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?
| Перевозчик | Стоимость перевозки одним автомобилем (руб. на 10 км) | Грузоподъемность автомобилей (тонн) |
| А | 2,2 | |
| Б | 2,8 | |
| В | 3,2 |
Решение.
Рассмотрим все варианты.
Для перевозки 3 тонн груза перевозчику A понадобится 2 автомобиля. Стоимость перевозки каждым из них составит 110 · 25 = 2750 руб. Полная стоимость перевозки 2 750 · 2 = 5500 руб.
Для перевозки 3 тонн груза перевозчику Б понадобится 2 автомобиля. Стоимость перевозки каждым из них составит 140 · 25 = 3500 руб. Полная стоимость перевозки 3 500 · 2 = 7000 руб.
Для перевозки 3 тонн груза перевозчику В понадобится 1 автомобиль. Стоимость перевозки составит 160 · 25 = 4000 руб.
Стоимость самой дешевой перевозки составит 4000 руб.
Ответ: 4000.
13. Задание 13 № 25655
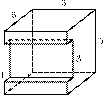 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Объем многогранника равен разности объемов куба, ребро которого равно 5, и прямоугольного параллелепипеда с ребрами 1, 3, 5, откуда находим: 53 − 1 · 3 · 5 = 110.
Ответ: 110.
14. Задание 14 № 512919
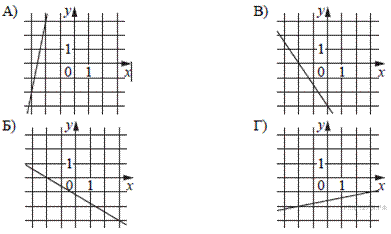
На рисунках изображены графики функций вида 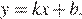 Установите соответствие между графиками функций и угловыми коэффициентами прямых.
Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) 0,2
2) 5
3) −1,5
4) −0,6
В таблице под каждой буквой укажите соответствующий номер.
| A | Б | В | Г |
Решение.
Если прямая задана уравнением 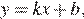 то при k > 0 функция возрастает, при k < 0 — убывает. Таким образом, имеем: A — 2, Б — 4, В — 3, Г — 1.
то при k > 0 функция возрастает, при k < 0 — убывает. Таким образом, имеем: A — 2, Б — 4, В — 3, Г — 1.
Ответ: 2431.
15. Задание 15 № 512423
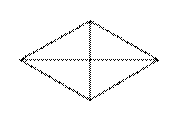
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 25. Найдите периметр ромба.
Решение.
Сумма двух углов ромба равна 120°, значит, каждый угол равен 120° : 2 = 60°. Сумма двух остальных углов ромба равна 360° − 120° = 240°, значит, каждый из них равен 240° : 2 = 120°. Меньшая диагональ ромба лежит напротив меньшего угла ромба 60°, поэтому получаем равносторонний треугольник, основанием которого является данная диагональ. Таким образом, периметр ромба равен 25 · 4 = 100.
Ответ: 100.
16. Задание 16 № 520564
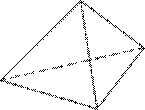 Стороны основания правильной треугольной пирамиды равны 8, а боковые рёбра равны 5. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной треугольной пирамиды равны 8, а боковые рёбра равны 5. Найдите площадь боковой поверхности этой пирамиды.
Решение.
Найдём апофему пирамиды:
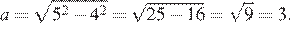
Найдём площадь боковой поверхности пирамиды:
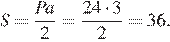
Ответ: 36.
17. Задание 17 № 514476
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ | |
А) 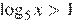 Б)
Б) 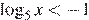 В)
В) 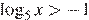 Г)
Г) 
| 1) 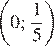 2)
2) 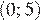 3)
3) 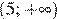 4)
4) 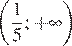
|
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.
| А | Б | В | Г |
Решение.
Заметим, что область допустимых значений, в каждом неравенстве: 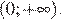 Основание логарифма больше единицы, поэтому при переходе от логарифмического неравенства к подлогарифмическому выражению знак меняться не будет.
Основание логарифма больше единицы, поэтому при переходе от логарифмического неравенства к подлогарифмическому выражению знак меняться не будет.
А) 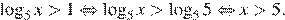
Б) 
В) 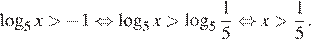
Г) 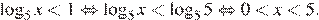
Ответ: 3142.
18. Задание 18 № 510904
Школа приобрела стол, доску, магнитофон и принтер. Известно, что принтер дороже магнитофона, а доска дешевле магнитофона и дешевле стола. Выберите утверждения, которые верны при указанных условиях.
1) Магнитофон дешевле доски
2) Принтер дороже доски
3) Доска ― самая дешёвая из покупок
4) Принтер и доска стоят одинаково
В бланк ответов запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение.
1) Магнитофон дешевле доски — неверно, противоречит условию «доска дешевле магнитофона».
2) Принтер дороже доски — верно: доска дешевле магнитофона, а принтер дороже магнитофона.
3) Доска ― самая дешёвая из покупок. Верно, так и есть.
4) Принтер и доска стоят одинаково — неверно, уже спрашивали в п. 2: принтер дороже.
----------
Только мы не поняли, что такое магнитофон, где его покупают и зачем.
19. Задание 19 № 512487
Найдите четырёхзначное число, большее 2000, но меньшее 3000, которое делится на 60 и сумма цифр которого равна 12. В ответе укажите какое-нибудь одно такое число.
Решение.
Представим искомое число в виде abcd. Если число делится на 60, то оно также делится на 3 и на 20. Так как сумма цифр искомого числа равна 12, то оно автоматически будет делиться на 3. Число делится на 20 тогда и только тогда, когда число оканчивается на ноль, а предпоследняя цифра четная. Так как число abcd < 3000, то a = 2, а сумма b + c + d = 10, и d должно быть обязательно равно нулю, с — обязательно четное. Рассмотрим все случаи.
Допустим, что с = 0, тогда b = 10, что невозможно в силу 
Допустим, что с = 2, тогда b = 8, откуда следует, что abcd = 2820 — искомое число.
Допустим, что с = 4, тогда b = 6, откуда следует, что abcd = 2640 — искомое число.
Допустим, что с = 6, тогда b = 4, откуда следует, что abcd = 2460 — искомое число.
Допустим, что с = 8, тогда b =2, откуда следует, что abcd = 2280 — искомое число.
Ответ: 2280, или 2460, или 2640, или 2820.
20. Задание 20 № 506688
Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?
Решение.
Последовательность цен за метр — арифметическая прогрессия с первым элементом 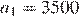 и разностью
и разностью 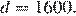 Сумма первых
Сумма первых 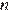 элементов арифметической прогрессии —
элементов арифметической прогрессии — 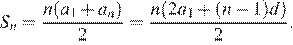 То есть в нашем случае имеем
То есть в нашем случае имеем 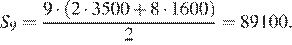
Примечание.
Цены завышены в несколько раз. Видимо, составители ЕГЭ никогда не рыли колодцев.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|