
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема. Применение основных тригонометрических тождеств.
Тема. Применение основных тригонометрических тождеств.
Краткие теоретические сведения
Основные тригонометрические тождества
sin2α +cos2α=1
sin α=+ 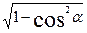  tgα =
tgα = 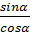 ctgα =
ctgα = 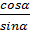
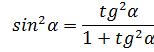
|
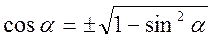
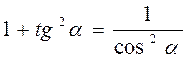 1 +
1 + 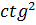 α = α = 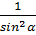
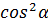 = = 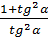 tgα
tgα 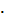 ctgα = 1 ctgα = 1
|
Рассмотрим решение нескольких примеров:
Пример1. Дробь 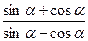 выразить через tg α и вычислить, если tg α=5.
выразить через tg α и вычислить, если tg α=5.
Решение: 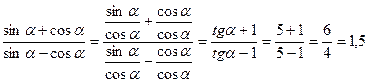
Каждый член дроби делим на сos 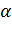 , так как нам известен tg
, так как нам известен tg 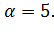
Пример2. Доказать тождество: 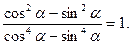
Решение: 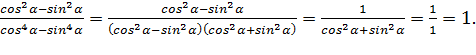
Знаменатель расписали как разность квадратов, далее идет сокращение на 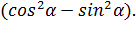
Пример3. Доказать тождество: 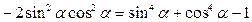 .
.
Решение: 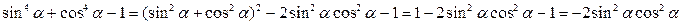
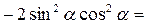
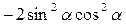
Пример4.Доказать тождество: 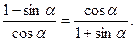
Решение. Используем свойство пропорции: произведение крайних равно произведению
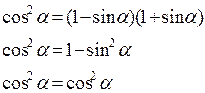 средних (умножение «крест накрест»):
средних (умножение «крест накрест»):
(произведение скобок сворачиваем как разность квадратов)
(используем формулу 1 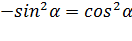 )
)
Задания для практической работы № 19
1уровень
1. Найдите значение выражения 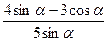 , если tg α=2.
, если tg α=2.
2. Вычислите: 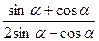 , если ctg α=3.
, если ctg α=3.
3. Упростите выражение: 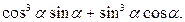
Рекомендации: вынесите множитель sin 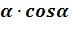 за скобки
за скобки
4. Упростите выражение: 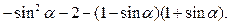
5. Упростите выражение: co 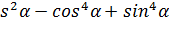 .
.
Рекомендации: первое и второе сгруппируйте, затем вынесите общий множитель за скобки.
2 уровень
6. Приведите к более простому виду выражение: 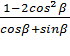
7. Докажите тождество: 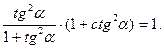
3 уровень
8. Упростить выражение: 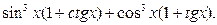
Контрольные вопросы:
1.Сформулируйте определение синуса, косинуса.
2. Какое наибольшее значение может принимать синус, косинус, тангенс?
3. Какое наименьшее значение может принимать синус, косинус, тангенс?
4. Могут ли синус и косинус одного и того же аргумента быть равными
соответственно: 0,6 и 0,8?
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|