Практические занятия от 03.11

Практические занятия от 03.11

Числовые ряды. Признаки сходимости числовых рядов с положительными членами и вычисление их сумм с заданной точностью.

1)Точное нахождение суммы ряда и использование простейших признаков сходимости

В пособии “Математический анализ в примерах и задачах, часть 2” (файл МА_П_3(часть2).pdf) ознакомиться с разделом 5.1 (c. 54 – 56) и из упражнений в конце раздела выполнить упражнения 5.1, 5.3, 5.5, 5.8, 5.10. (При выполнении упражнения 5.8 следует разложить общий член ряда на простейшие дроби и найти явное выражение для частичной суммы ряда, затем перейти к пределу при )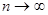

2)Признаки сравнения. Интегральный признак сходимости ряда.

В том же пособии ознакомиться с разделом 5.2 (c. 57 – 60) (с разбором всех приведенных примеров, но можно без упражнений).

3)Признаки сходимости Даламбера и Коши.

В том же пособии в разделе 5.3 повторить формулировки соответствующих теорем, которые были также в последней лекции (в данном пособии это Теоремы 5.6 и 5.7 на c. 62) и проследить разбор примеров 5.13 и 5.15, а также выполнить упражнения 5.42 и 5.53 на с. 63.

4)Вычисление сумм рядов с заданной точностью.

Посмотрите еще раз материалы к последним лекциям – разделы 10.3 и 10.4 в пособии “Математический анализ” (файл Мат.ан.2013.pdf). В этих разделах проследите разбор примеров 10.4 (с. 91), 10.5 и 10.6 (с. 93-94).

Иногда при использовании интегрального признака сходимости удобно рассматривать не само выражение общего члена ряда, а его верхнюю оценку (начиная с некоторого номера), для которой легче найти интеграл. Рассмотрим следующий пример.

Доказать сходимость ряда 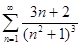и вычислить его сумму с точностью до 0.001.

Поскольку общий член ряда представляет собой рациональную дробь от n, признаки Даламбера и Коши здесь работать не будут (в соответствующих пределах будет получаться 1). Остается использовать интегральный признак. Но интеграл от данной рациональной дроби вычисляется очень сложно, поэтому воспользуемся верхней оценкой общего члена ряда, такой, чтобы в числителе была производная от внутренней функции знаменателя, например 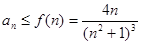при 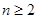. Нетрудно проверить, что при 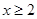функция 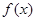является убывающей и ее первообразная 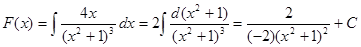. Поскольку 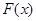очевидно имеет конечный предел на бесконечности, 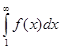сходится, следовательно по интегральному признаку сходится ряд 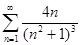, следовательно исходный ряд сходится по признаку сравнения. Кроме того, при остаток исходного ряда 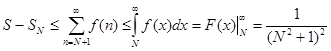. Таким образом, для приближенного вычисления исходного ряда с точностью до 0.001 достаточно, чтобы число слагаемых частичной суммы 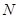было не меньше 2 и удовлетворяло неравенству 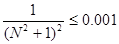, или 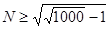. Таким образом, для вычисления суммы ряда с заданной точностью достаточно взять 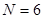слагаемых.

Типовой расчет

Вместе с данными материалами высылаю варианты типового расчета по рядам. Номер вашего варианта определяется двумя последними цифрами номера зачетной книжки (если 31, то 1, если 32, то 3). Пока делайте только часть a), часть b) разберем позднее. Для каждого ряда в части a) нужно доказать сходимость и вычислить сумму с заданной точностью, определив нужное число слагаемых. Срок выполнения всего ТР – не позднее 8 декабря.