
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЛЕКЦИЯ № 20. МЕТОДЫ ИНТЕГРИРОВАНИЯ
ЛЕКЦИЯ № 20
МЕТОДЫ ИНТЕГРИРОВАНИЯ
по дисциплине Математика
Раздел 3. Интегральное исчисление функции одной переменной
Тема 7. Неопределенный интеграл
Учебная цель: формировать знания о методах интегрирования заменой переменной и по частям в неопределенном интеграле, об интегрировании выражений, содержащих квадратный трехчлен.
Учебные вопросы:
1. Замена переменной в неопределенном интеграле.
2. Интегрирование по частям.
Литература:
1. Высшая математика для экономистов : учебник / под ред. Н. Ш. Кремера. – М. : ЮНИТИ, 2006.
2. Письменный, Д. Т. Конспект лекций по высшей математике : в 2 ч. Ч. 1 / Д. Т. Письменный. - М. : Айрис-пресс, 2003.
Санкт – Петербург
Вопрос 1. Замена переменной в неопределенном интеграле.
Цель этого метода – свести исходный интеграл к более простому для вычисления интегралу.
Пусть дан интеграл 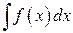 , пусть функция
, пусть функция 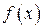 непрерывна на интервале
непрерывна на интервале 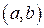 и
и 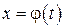 - непрерывно дифференцируема на интервале
- непрерывно дифференцируема на интервале 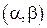 .
.
В силу свойства инвариантности неопределенного интеграла можно записать
( 1 ) 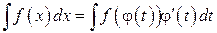 ,
, 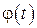 - монотонна.
- монотонна.
Пусть
( 2 ) 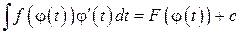 .
.
Чтобы вернуться к переменной х нужно из уравнения 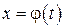 выразить t через х и подставить в (2).
выразить t через х и подставить в (2).
Если 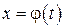 не является монотонной, то возвращение от t к х может быть сопряжено с большими трудностями. Поэтому формулу (1) применяют для монотонных функций.
не является монотонной, то возвращение от t к х может быть сопряжено с большими трудностями. Поэтому формулу (1) применяют для монотонных функций.
Примеры
1. 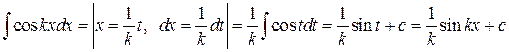
2. 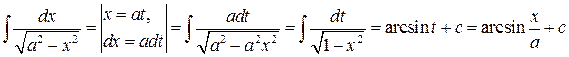
3. 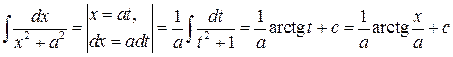
4. 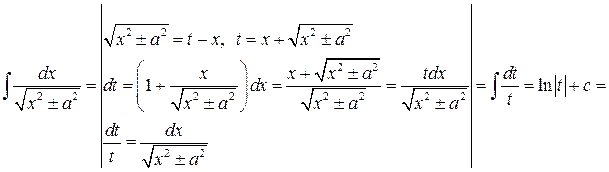
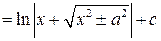
Замечание. На практике часто замену делают не в виде 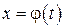 , а
, а 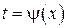 .
.
Пример
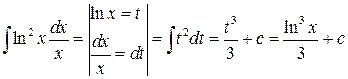 .
.
Вопрос 2. Интегрирование по частям.
Пусть дан интеграл вида 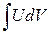 , где
, где 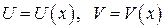 - непрерывно дифференцируемые функции.
- непрерывно дифференцируемые функции.
Рассмотрим
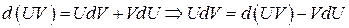 ,
,
проинтегрируем обе части равенства
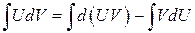
или окончательно
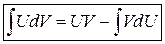 -
-
- формула интегрирования по частям.
Таким образом, вычисление интеграла 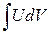 приводится к вычислению интеграла
приводится к вычислению интеграла 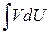 , который может оказаться более простым или вообще табличным.
, который может оказаться более простым или вообще табличным.
Примеры
1. 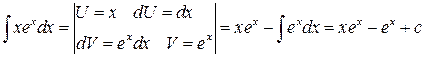
2. 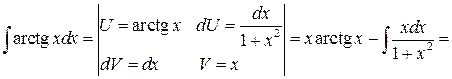
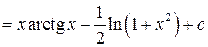
Пусть 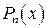 - многочлен степени n. Методом интегрирования по частям можно вычислить, например, интегралы вида:
- многочлен степени n. Методом интегрирования по частям можно вычислить, например, интегралы вида:
1 группа:
1) 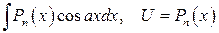
2) 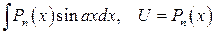
3) 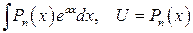
4) 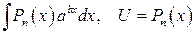
2 группа:
1) 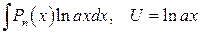
2) 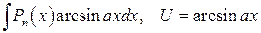
3) 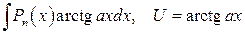
4) 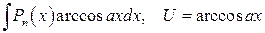
3 группа:
1) 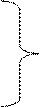 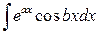 2)
2) 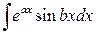 3)
3) 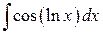 4)
4) 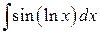
| Обозначая любой из интегралов этой группы через 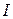 и производя двукратное интегрирование по частям, мы составим для и производя двукратное интегрирование по частям, мы составим для 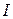 уравнение первого порядка. уравнение первого порядка.
|
Пример
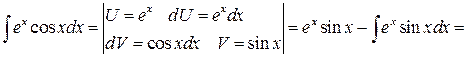
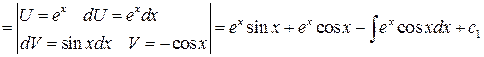
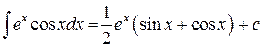
Замечание 1. Интегралы 1-ой группы берутся путем n-кратного применения формулы интегрирования по частям, причем в качестве 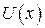 всякий раз берется многочлен, степень которого уменьшается после каждого интегрирования по частям.
всякий раз берется многочлен, степень которого уменьшается после каждого интегрирования по частям.
Пример
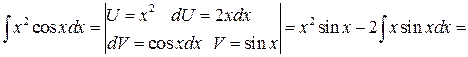
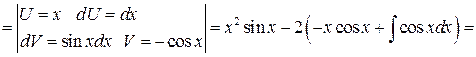
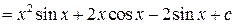
Замечание 2. Три перечисленные группы не исчерпывают всех интегралов, берущихся посредством интегрирования по частям.
Пример
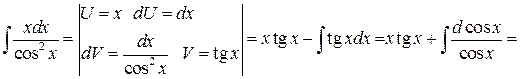

Выводы.
1. Метод замены переменной – один из основных методов вычисления неопределенного интеграла, цель метода - свести исходный интеграл к более простому для вычисления интегралу.
2. Метод интегрирования по частям применяется к интегрированию выражений вида 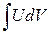 , где
, где 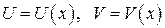 - непрерывно дифференцируемые функции.
- непрерывно дифференцируемые функции.
Текст лекции разработал:
доцент кафедры №1 Пушкина В.П.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|