
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Координатно-векторный метод. Координаты вершин многогранников.. А (0,0,0), А1(0,0,1), В(1,0,0), В1(1,0,1), D( 0 ,1 ,0), D1( 0,1,1), С(1,1,0), С1(1,1,1).. А (0,0,0), А1(0,0,1), В(1,0,0), В1(1,0,1), С(0,5; ,0), С1(0,5; ,1).
Координатно-векторный метод
Уравнение плоскости имеет видAx + By + Cz + D= 0, где  - нормаль к плоскости. Если даны три точки, то решается система из трех уравнений.
- нормаль к плоскости. Если даны три точки, то решается система из трех уравнений.
1. Угол между прямыми a и b, где  и
и 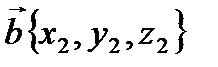 - направляющие векторы
- направляющие векторы

2. Угол между прямой а и плоскостьюAx + By + Cz + D= 0, где  - направляющий вектор прямой а,
- направляющий вектор прямой а,  - нормаль к плоскости
- нормаль к плоскости
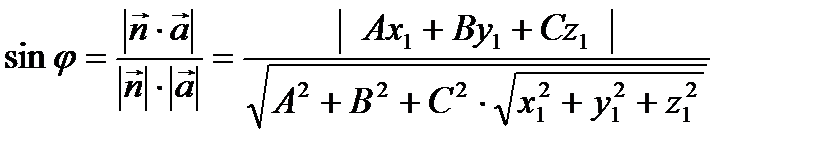
3. Угол между плоскостями A1x + B1y + C1z + D1= 0 и A2x + B2y + C2z + D2= 0 (это угол между нормалями 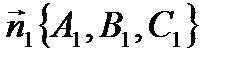 и
и 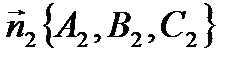 этих плоскостей)
этих плоскостей)

4.Расстояние между точками А(x1 ,y1, z1) и В(x2 ,y2, z2)
 =
= 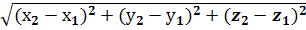 .
.
5.Расстояние от точки M0(x0 ,y0, z0), до плоскости Ax + By + Cz + D= 0
h= 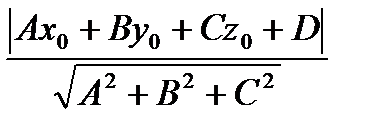
6.Если отрезок, концами которого служат точки А(x1 ,y1, z1) и В(x2 ,y2, z2) разделен точкой С(х, у, z) в отношении λ, то координаты точки С определяются по формулам x =  ; у=
; у= 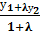 ; z=
; z= 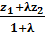 .
.
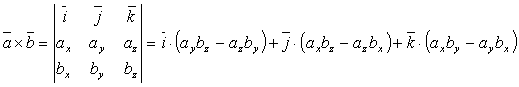
вычислить требуемое расстояние от точки до прямой в пространстве по формуле
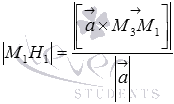
Координаты вершин многогранников.
1. Единичный куб A...D1
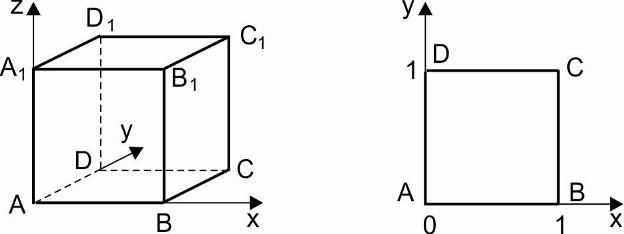
А (0,0,0), А1(0,0,1), В(1,0,0), В1(1,0,1), D( 0 ,1 ,0), D1( 0,1,1), С(1,1,0), С1(1,1,1).
2. Правильная треугольная призма A…C1 , все ребра, которой равны 1.

А (0,0,0), А1(0,0,1), В(1,0,0), В1(1,0,1), С(0,5; ,0), С1(0,5; ,1).
3. Правильная шестиугольная призма A...F1, все ребра которой равны 1.
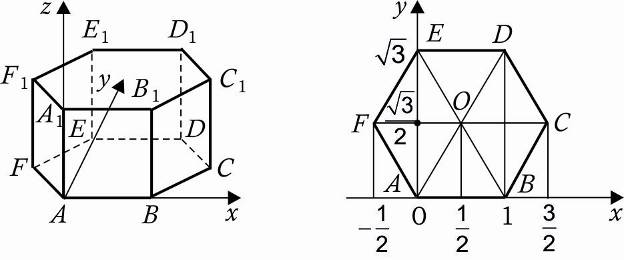
А (0,0,0), А1(0,0,1), В(1,0,0), В1(1,0,1),
С(1,5; 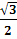 ,0), С1(1,5;
,0), С1(1,5; 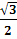 ,1), D(1,
,1), D(1, 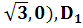 (1,
(1, 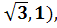 Е(0,
Е(0, 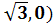 ,
,  (0,
(0, 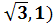 , F(-05,
, F(-05, 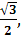 0),
0),
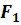 (-05,
(-05, 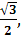 1).
1).
4. Правильная треугольная пирамида (тетраэдр) ABCD, все ребра которой равны 1. 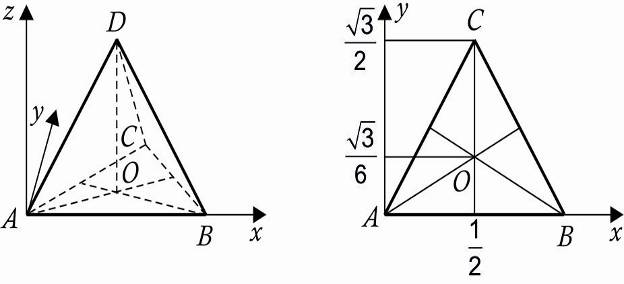
А (0,0,0),В(1,0,0),С(0,5; 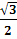 ,0), D(0,5,
,0), D(0,5, 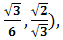
5. Правильная четырехугольная пирамида SABCD, все ребра которой равны 1.
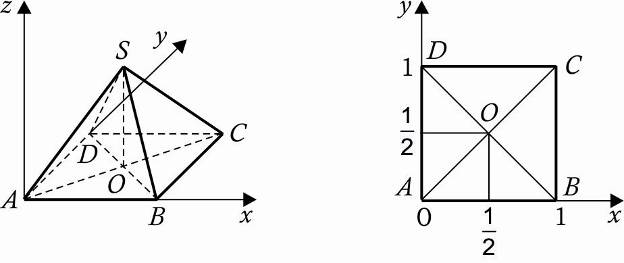
А (0,0,0),В(1,0,0),С(1,1,0), D(0,1,0 S(0,5;0,5; ).
6. Правильная шестиугольная пирамида SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2.
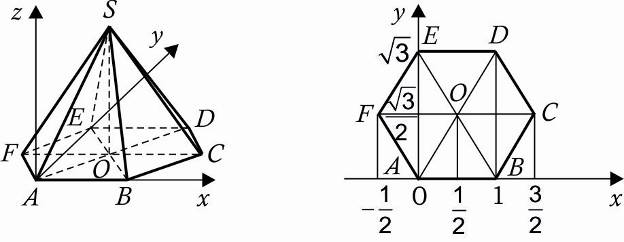
А (0,0,0), В(1,0,0),С(1,5; ,0), D(1, Е(0, , F(-05, 0), S(0,5; ).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|