Выбор модулей

2N²+1<= M

N = sqrt((M-1)/2)

m1 = 10^6

m2 = 10^6

n = 20

M = (10^6)^20 = 10^120

Пример оценки порядка дроби Фарея

результата суммирования k дробей

Сложение двух дробей

C = A₁/B₁ + A₂/B₂= (A₁B₂+A₂B₁)/(B₁B₂)

|A₁|<=N, |A₂|<=N, |B₁|<=N, |B₂|<=N

Числитель C <= 2N², а знаменатель - N²

Сложение трёх дробей

C = A₁/B₁ + A₂/B₂+ A₃/B₃ = (A₁B₂ B₃+A₂B₁ B₃+ A₃B₁ B₂)/(B₁B₂ B₃)

Числитель C <= 3N³, а знаменатель - N³

Сложение k дробей

Числитель C <= kN^k, а знаменатель - N^k

0,123 = 123 ∙ 10^-3

1. Параметры модулярной системы счисления

p₁ = 2, p₂ = 3, p₃ = 5

k_f = 2 n_f = 3

2. Преобразование в модулярную систему счисления

А₁ = К₁ ∙ 10^t¹ (1)

А₂ = К₂ ∙ 10^t²

А₁ = 1 ∙ 10¹

А₂ = 2 ∙ 10²

К₁ = (1,1,1)

К₂= (0,2,2)

А₁ = [(1,1,1), 1]

А₂ = [(0,2,2), 2]

3. Рассмотрим их умножение

А₃ = А₁∙ А₂ = К₁ ∙ К₂ ∙ 10^t¹⁺^t² = [(0,2,2), 3]

4. Рассмотрим сложение

А₄ =К₁ ∙ 10^t¹ + К₂ ∙ 10^t2 =

Пусть t1<t2, тогда

А₄ = 10^t¹∙(К₁ + К₂ ∙ 10^t2^-^t1) =

А₄ = [(1 + 0∙10¹, 1 + 2∙10¹, 1 + 2∙10¹), 1] =

[(1,21,21),1] = [(1,0,1),1]

5. Рассмотрим вычитание

А₅ =К₁ ∙ 10^t¹ - К₂ ∙ 10^t2 =

Пусть t1<t2, тогда

А₅ = 10^t¹∙(К₁ - К₂ ∙ 10^t2^-^t1) =

А₅ = [(1 - 0∙10¹, 1 - 2∙10¹, 1 - 2∙10¹), 1] =

= [(1,-19,-19),1] = [(1,2,1),1]

6 Обратное преобразование

А₃ = [(0,2,2),3]

Р = 2 ∙ 3 ∙ 5 = 30

Определяем базисы:

Р/ p₁ = 15, m₁ = 15^-1 mod p₁ = 1

Р/ p₂ = 10, m₂ = 10^-1 mod p₂ = 1

Р/ p₃ = 6, m₃ = 6^-1 mod p₃ = 1

B₁ = 15, B₂ = 10, B₃ = 6

B₁ = (1,0,0); B₂ = (0,1,0); B₃ = (0,0,1)

К₃ = 0∙15+2∙10+2∙6 = 32 mod 30 = 2

А₃ = 2∙10³.

Преобразуем

А₄ = [(1,0,1),1]

K₄ = 1∙15+0∙10+1∙6 = 21 mod 30 = 21

А₃ = 21∙10¹.

Преобразуем

А₅ = [(1,2,1),1]

K₅ = 1∙15 + 2∙10 + 1∙6 = 41 mod 30 = 11

А₅ = 11∙10¹, но точный результат (-19) ∙10¹

Псевдопереполнение!

Рассмотрим следующий пример:

А₆ = 1 ∙ 10⁰- 5 ∙ 10⁰ = -4∙ 10⁰

А₆ = [(1, 1, 1), 0] - [(1, 2, 0), 0] = [(0, 2, 1), 0]

K₆ = 0∙15 + 2∙10 + 1∙6 = 26 mod 30 = 26

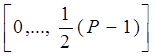= [0, 14] для полож. Чисел

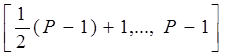= [15,30] для отрицат чисел

26 соответствует отрицательному числу, которое определяется по формуле –(Р-26) = -4

Выбор модулей

Утвержение. Для того чтобы не было псевдопереполнения порядок дробей Фарея результата не должен превосходить Р/2.

r = 10 – 10 цифр

[-9,-8,…,0,…9] – 19 цифр

[99 99]

99 = -9*10¹+ (-9) = -90 – 9 = -99

99+99+1 = 199 чисел

В двоичной системе счисления

r^2

19^2 = 361

(01) = (19) = 1*10⁰-9

Рассмотрим пример сложения двух чисел 3645 и 1456 при

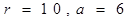Избыточная система счисления с цифрами от -6 до 6.

с = [ 0 1 1 1]

u = [ 4 0 1 1]

3 2 1 0

3 6 4 5 (x)

+ 1 4 5 6 (y)
0 1 1 1 (c)

4 0 1 1 (u)
5 1 0 1 (s)

S0=u0

S1= u1 + c0

s2=u2 + c1

s3 = u3 + c2