Хелпикс

Главная

Контакты

Случайная статья



UCm(-) → uC (-) (t) )=| UCm(-) | sin(ωt +arg UCm(-))



 

Комбинированный метод расчета переходных процессов (метод Богатырева)

 при наличии гармонических источников

 

Комбинированный метод заключается в раздельном расчете принужденной и свободной составляющих переходных процессов. Принужденная составляющая рассчитывается классическим методом, а свободная – операторным. Метод наиболее удобен для расчета переходных процессов при синусоидальных воздействиях и основан на теореме наложения.

I – принужденная составляющая (классический метод) и                II – свободная составляющая (операторный метод)                        накладываются друг на друга

 

АЛГОРИТМ

1. Расчет принужденного режима  (метод комплексных амплитуд)

Рассчитываются принужденные составляющие

-искомой величины I пр m→ iпр(t) = | I пр m| sin(ωt +arg I пр m)

-ток индуктивности ILпр m→ iLпр(t) =| ILпр m | sin(ωt + arg ILпр m)

-напряжение на конденсаторе

                                 UCпр m → uCпр(t)=|UCпр m| sin(ωt +arg UCпр m)

Сначала в комплексах, затем переводятся в мгновенные (временные) значения.

При t=0 получают значения uCпр (0) и iLпр (0)

2. Расчет до коммутации ( 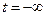) (метод комплексных амплитуд)

Из анализа установившегося режима до коммутации находят:

- ток индуктивности ILm(-) → iL(-) (t) =| ILm(-) | sin(ωt + arg ILm(-) )

- напряжение на конденсаторе

UCm(-) → uC (-) (t) )=| UCm(-) | sin(ωt +arg UCm(-))

Получают значенияuC (-) (0) и iL (-)(0)

3. Определение независимых начальных условий:

используют результаты п.2 uC(0) = uC (0-) ,  iL(0) = iL(0-)

4.Вычисление свободныхсоставляющих независимых начальных условий   uCсв(0) = uC (0) – uCпр(0)

               iLсв(0) = iL(0) – iLпр(0)

5. Составляется операторная схема для изображений свободных составляющих.

В операторной схеме все источники входных сигналов исключаются. На их месте остаются только внутренние сопротивления (если идеальные источники, то на месте ЭДС – закоротка, источника тока – разрыв. В схеме действуют только источники, учитывающие внутреннюю энергию, накопленную в индуктивности и в конденсаторе до коммутации 

                       iLсв(0)L  и  uCсв(0)/p

6. Расчет операторной схемы относительно изображений свободных составляющих искомых величин. Ответ получаем в виде правильной дроби – отношения полиномов.

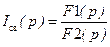
7. Переход к оригиналам свободных составляющих искомых величин.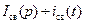

Определяем оригиналы искомых величин по изображениям посредством теоремы разложения.

Формула разложения Хэвисайда: ,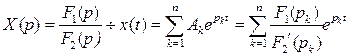

где pk-корни уравнения ,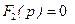

для случая комплексно-сопряженных корней 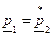формуларазложения имеет вид

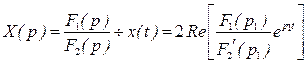
8. Результат – наложение принужденного и свободного режимов i(t)=iпр(t)+ iсв(t)

 

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.