Сфера – это поверхность шара. Сфера не является телом.. Изображения сферы и шара не отличаются.. Сечения. Задания тренировочного модуля

УРОК 98. 04.05.20 ТЕМА. ШАР. СФЕРА.

Этапы работы	Шар	Сфера	Примечание
1. Определение	Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не больше данного от данной точки.

Сфера – это поверхность шара

Сфера не является телом.

2. Изображения

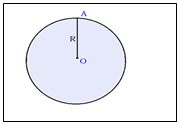
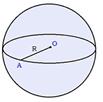
Изображения сферы и шара не отличаются.

3. Основные элементы

Центр шара (сферы)- точка О

Радиус шара (сферы)- R

Диаметр шара (сферы)- D=2R.

Сечения

Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара).

Секущая плоскость сферы: окружность.

Секущая плоскость шара: круг, который имеет площадь и не имеет длины окружности.

5.Расстояние до секущей плоскости

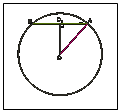
В вычислениях используется теорема Пифагора в прямоугольном треугольнике AOO₁.

OO₁ =d — расстояние между центром шара и плоскостью сечения;

OA=R — радиус шара;

O₁A = r — радиус окружности сечения.

6. Формулы

Площадь поверхности шара (т. е. сферы) вычисляется по формуле S(сферы)= 4⋅π⋅R², где R — радиус шара.

Объём шара вычисляется по формуле V(шара)= ⋅π⋅R³, где R — радиус шара.

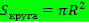- площадь круга

-длина окружности

Задания тренировочного модуля

1.Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Решение:

Площадь круга вычисляется по формуле: S_кр=πR².

Площадь поверхности шара вычисляется по формуле: S_сф=4πR². Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

Ответ: 36 кв. м.

3. Радиус сферы равен 25 см. Сфера пересечена плоскостью, которая находится на расстоянии 20 см от центра сферы.

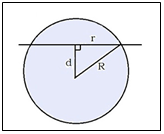Вычисли радиус окружности сечения.

По теореме Пифагора: r²=R²−d²;

R= 25 см и d= 20 см;

r²=25²−20²;

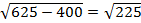
r= 15 см.

Ответ:15 см

2.Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Решение:

Площадь сферы равна S_сф=4πR². То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r² =100, то есть r=10.

Ответ: 10.

1.Радиус сферы равен 13 см. Сфера пересечена плоскостью, которая находится на расстоянии 5 см от центра сферы.

Вычисли радиус окружности сечения.

2. Дан радиус сферы R= 18 см. Определи площадь поверхности сферы.

3. Дана площадь поверхности сферы 144πсм². Определи диаметр сферы.

Для самостоятельного решенияКонец формы