
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
п.3. Формула Байеса
Тема 1.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ, ФОРМУЛА БАЙЕСА
План лекции:
- Независимость событий.
- Формула полной вероятности.
- Формула Байеса.
п.1. Независимость событий
Если при наступлении события 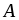 вероятность события
вероятность события 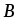 не меняется, то события
не меняется, то события 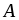 и
и 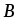 называются независимыми.
называются независимыми.
Теорема: Вероятность совместного появления двух независимых событий 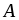 и
и 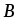 (произведения
(произведения 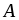 и
и 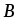 ) равна произведению вероятностей этих событий.
) равна произведению вероятностей этих событий.
Доказательство: События 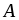 и
и 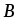 независимы, следовательно
независимы, следовательно 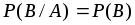 . В этом случае формула произведения событий
. В этом случае формула произведения событий 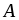 и
и 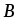
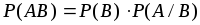 можно записать как
можно записать как 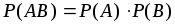 .
.
События 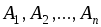 называются попарно независимыми, если независимы любые два из них.
называются попарно независимыми, если независимы любые два из них.
События 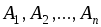 называются независимыми в совокупности, если каждое из этих событий и событие равное произведению любого числа остальных событий, независимы.
называются независимыми в совокупности, если каждое из этих событий и событие равное произведению любого числа остальных событий, независимы.
Теорема: Вероятность произведения конечного числа независимых в совокупности событий 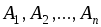 равна произведению вероятностей этих событий.
равна произведению вероятностей этих событий.
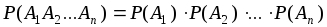 .
.
Простейшие свойства вероятностей:
-
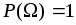 ;
; -
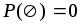 ;
; -
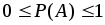 ;
; -
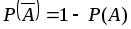 ;
; -
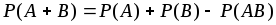 ;
;
Свойства условных вероятностей
-
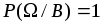 ;
; -
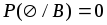 ;
; -
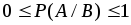 ;
; - если
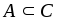 , то
, то 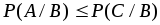 ;
; -
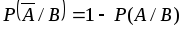 ;
; -
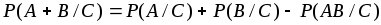 ;
; -
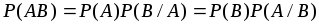 ;
; -
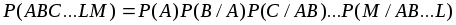 .
.
п.2. Формула полной вероятности
Теорема 1 (формула полной вероятности). Пусть события 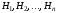 образуют полную группу несовместных событий. Будем эти события называть гипотезами. Тогда вероятность любого события
образуют полную группу несовместных событий. Будем эти события называть гипотезами. Тогда вероятность любого события  того же поля событий равна:
того же поля событий равна:
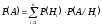
Доказательство. Так как события 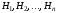 образуют полную группу событий, то событие
образуют полную группу событий, то событие  можно представить в виде:
можно представить в виде: 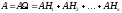 (это означает, что событие может произойти А только вместе с одним из событий
(это означает, что событие может произойти А только вместе с одним из событий 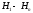 ). Так как события
). Так как события 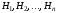 несовместны то:
несовместны то:
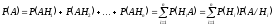
Пример 1. Детали поступают на конвейер с трех станков. Первый станок производит 25% всех деталей, второй 35% и третий 40% деталей. Первый станок выпускает 1% бракованных деталей, второй 3% , третий 5%. Определить вероятность того, что случайно выбранная с конвейера деталь окажется бракованной.
Решение. Введем обозначения событий:  - деталь окажется бракованной; события
- деталь окажется бракованной; события 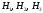 - деталь изготовлена соответственно первым, вторым или третьим производителем. По условию задачи:
- деталь изготовлена соответственно первым, вторым или третьим производителем. По условию задачи:
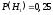 ,
, 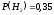 ,
, 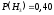 ;
;
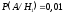 ,
, 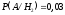 ,
, 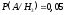 .
.
По формуле полной вероятности находим:
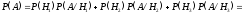
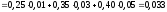
п.3. Формула Байеса
Теорема 2 (формула Байеса).Пусть событие  , которое могло произойти вместе с одним из событий
, которое могло произойти вместе с одним из событий 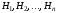 , образующих полную группу несовместных событий, наступило. Тогда условная вероятность того, что осуществилась гипотеза
, образующих полную группу несовместных событий, наступило. Тогда условная вероятность того, что осуществилась гипотеза 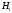 равна:
равна:
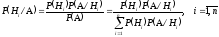
Поскольку данная формула позволяет вычислить апостериорные вероятности по априорным, то ее также называют формулой переоценки гипотез.
Доказательство. По определению условной вероятности:
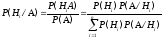 .
.
Пример 3. В условиях примера 1 определить вероятность того, что взятая деталь была изготовлена на первом станке, если она оказалась бракованной.
Решение. Требуется переоценить вероятность гипотезы 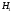 . По формуле Байеса имеем:
. По формуле Байеса имеем:
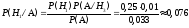 .
.
Вероятность стала меньше, поскольку если деталь оказалась бракованной, то более вероятно, что она произведена вторым, либо третьим станком.
Пример 4. В корзине находится один шар - с равной вероятностью белый или черный. В корзину опускается белый шар, и после перемешивания извлекается один шар. Он оказался белым. Какова вероятность, что в корзине остался белый шар.
Решение.Пусть гипотеза 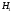 - в корзине исходно находится белый шар, гипотеза
- в корзине исходно находится белый шар, гипотеза 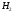 - в корзине находится черный шар. Так как с равной вероятностью в корзине может находиться как белый, так и черный шар, то:
- в корзине находится черный шар. Так как с равной вероятностью в корзине может находиться как белый, так и черный шар, то: 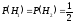 . После того, как в корзину был опущен белый шар, вероятность вынуть белый шар (событие
. После того, как в корзину был опущен белый шар, вероятность вынуть белый шар (событие  ) в предположении гипотезы
) в предположении гипотезы 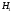 есть:
есть: 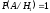 . Аналогично, вероятность вынуть белый шар в предположении гипотезы
. Аналогично, вероятность вынуть белый шар в предположении гипотезы 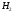 :
: 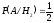 . Следовательно по формуле полной вероятности:
. Следовательно по формуле полной вероятности:
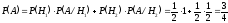 .
.
Тогда вероятность, что в корзине остался белый шар (то есть верна гипотеза 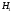 ):
):
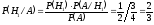 .
.
Пример 5. Два стрелка стреляют по мишени, делая по одному выстрелу. Вероятность попадания для первого стрелка 0,8, для второго – 0,4. После стрельбы в мишени обнаружена только одна пробоина. Найти вероятность того, что попал первый стрелок.
Решение.Некоторая сложность в данной задаче состоит в том, что мы уже решали аналогичную прямую задачу, не привлекая при этом формулу полной вероятности.
Введем обозначения: 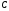 - попал в цель только один стрелок,
- попал в цель только один стрелок,  первый стрелок попал в цель,
первый стрелок попал в цель,  -второй стрелок попал в цель. Тогда:
-второй стрелок попал в цель. Тогда: 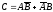 . То есть, можно считать, что событие
. То есть, можно считать, что событие 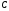 может наступить в результате осуществления двух гипотез:
может наступить в результате осуществления двух гипотез: 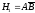 - попал в цель только первый стрелок,
- попал в цель только первый стрелок, 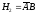 - попал в цель только второй стрелок. Имеем:
- попал в цель только второй стрелок. Имеем: 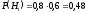 ,
, 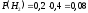 ,
, 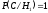 ,
, 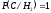 .
.
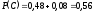 .
. 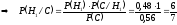 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|