Практическое занятие №18.. Расчетное задание «Приложение определенного интеграла к решению задач». Текст задания.. Вариант №1. Уровень А.. Уровень В.. Уровень С.. Вариант №2. Уровень А.. Уровень В.. Уровень С.

Практическое занятие №18.

Тема: Определенный интеграл.

Расчетное задание «Приложение определенного интеграла к решению задач»

Цель:сформировать навыки вычисления определенных интегралов, развивать умение решать прикладные задачи с помощью интегралов.

1) Текст задания.

Вариант №1

Уровень А.

А1.. Вычислите интеграл:

а) 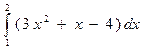; б) .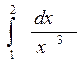

А2.Для функции f(x) = 3sin x найдите:

а) множество всех первообразных;

б) первообразную, график которой проходит через точку М ( 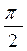; 0 )

А3.Вычислите, сделав предварительно рисунок, площадь фигуры, ограниченной линиями:

у = 0,5 х², у = 0, х = 2, х = 0.

А4. Скорость движения тела задается формулой 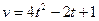(м/с). Найти путь, пройденный телом за 4 с от начала движения.

Уровень В.

В5.Вычислите интеграл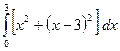

Уровень С.

С6.Найдите площадь фигуры, ограниченной линиями у = 6х – х² и у = 2х.

Вариант №2

Уровень А.

А1.. Вычислите интеграл:

а) 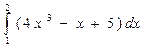; б) .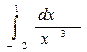

А2.Для функции f(x) = 2cos x найдите:

а) множество всех первообразных;

б) первообразную, график которой проходит через точку М ( 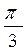; 0 )

А3.Вычислите, сделав предварительно рисунок, площадь фигуры, ограниченной линиями:

у = 2 х², у = 0, х = 3, х = 0.

А4. Скорость движения тела задается формулой 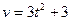(м/с). Найти путь, пройденный телом за 5 с от начала движения.

Уровень В.

В5.Вычислите интеграл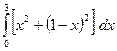

Уровень С.

С6.Найдите площадь фигуры, ограниченной линиями у = - 6х – х² и у = - 2х.