
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Докажите, что если медиана треугольника является его высотой, то треугольник равнобедренный.
24.11.20.Тема: Медианы, биссектрисы и высоты треугольника.
Повторите стр.32-35
Ознакомьтесьс образцами решения задач, перепишите в рабочую тетрадь или вклейте распечатанный текст.
№110.Докажите, что если медиана треугольника является его высотой, то треугольник равнобедренный.

 В
В
А С
D
Дано: 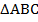 , BD - высота, медиана.
, BD - высота, медиана.
Доказать: 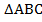 - равнобедренный.
- равнобедренный.
Доказательство.
Так как BD - высота, то 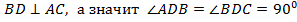 .
.
Так как BD - медиана, то AD= DC.
Так как 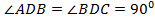 , AD= DC,BD- общая сторона, то ΔABD=ΔBDC по I признаку равенства треугольников. Тогда в равных треугольниках против равных прямых углов лежат равные стороны АВ и ВС.
, AD= DC,BD- общая сторона, то ΔABD=ΔBDC по I признаку равенства треугольников. Тогда в равных треугольниках против равных прямых углов лежат равные стороны АВ и ВС.
Если АВ = ВС, то по определению ΔАВС - равнобедренный.
№111.

 А
А
 |
С В
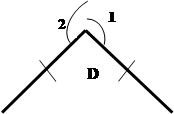
Дано: ΔАВС, CD=BD, 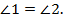
Доказать: 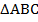 - равнобедренный.
- равнобедренный.
Доказательство.
CD=BD, 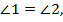 AD- общая сторона. Тогда ΔСDA=ΔADB по I признаку равенства треугольников. Против равных углов 1 и 2 в равных треугольниках лежат равные стороны АВ и АС соответственно.
AD- общая сторона. Тогда ΔСDA=ΔADB по I признаку равенства треугольников. Против равных углов 1 и 2 в равных треугольниках лежат равные стороны АВ и АС соответственно.
Так как АВ = АС, то 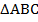 - равнобедренный по определению.
- равнобедренный по определению.
№112 .
 |



 2 А В
2 А В
 | |||
 | |||


С
Дано: АВ=ВС, 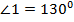 .
.
Найти: 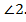
Решение.
Так как АВ=ВС, то по определению ΔАВС- равнобедренный.
По свойству углов равнобедренного треугольника 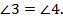
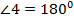 -
- 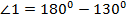 =
= 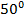 по свойству смежных углов.
по свойству смежных углов.
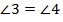 =
= 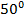 по свойству вертикальных углов.
по свойству вертикальных углов.
Ответ: 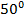
№ 114. Задача - теорема. Докажите, что в равных треугольниках, медианы проведенные к равным сторонам, равны (выучить формулировку наизусть).
В






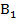
 |


 D
D 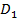
 А
А
 С
С 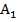
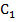
Дано: ΔАВС=Δ 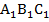 , AD и
, AD и 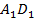 - медианы к сторонам ВС и
- медианы к сторонам ВС и 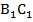 , ВС=
, ВС= 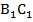 .
.
Доказать: AD = 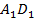 .
.
Доказательство:
Так как AD и 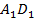 - медианы к сторонам ВС и
- медианы к сторонам ВС и 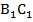 , то BD= DC и
, то BD= DC и 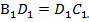
Так как ВС= 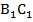 , то BD= DC=
, то BD= DC= 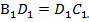
Так как ΔАВС=Δ 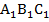 ,
, 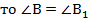 ,АВ =
,АВ = 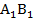 .
.
Так как 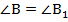 ,АВ =
,АВ = 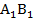 , BD=
, BD= 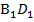 , то ΔАВD=Δ
, то ΔАВD=Δ 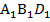 по первому признаку равенства треугольников.
по первому признаку равенства треугольников.
Против равных углов 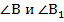 в равных треугольниках ΔАВD и Δ
в равных треугольниках ΔАВD и Δ 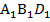 лежат равные стороны AD и
лежат равные стороны AD и 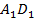 .
.
Домашнее задание
Повторите стр.32-35.
Решите№116(задача- теорема),№118.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|