
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Теоремы сложения и умножения вероятностей
ЛД1-191-ОТ – 02.11.2020
Тема: Теоремы сложения и умножения вероятностей
Задача № 2. Студент разыскивает нужную ему формулу в четырех справочниках. Вероятность того, что он отыщет её в первом справочнике, равна 0,6; во втором – 0,7; в третьем – 0,8; в четвертом – 0,8. Какова вероятность того, что:
а) он найдёт её во всех четырех справочниках;
б) он найдёт её в первом и четвёртом справочниках;
в) он найдёт её в трёх справочниках;
г) он найдёт её хотя бы в одном справочнике.
Решение.
а) 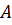 – студент найдет формулу во всех 4-х справочниках.
– студент найдет формулу во всех 4-х справочниках.
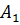 – студент найдет формулу в 1-ом справочнике;
– студент найдет формулу в 1-ом справочнике;
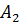 – студент найдет формулу во 2-ом справочнике;
– студент найдет формулу во 2-ом справочнике;
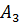 – студент найдет формулу в 3-ом справочнике;
– студент найдет формулу в 3-ом справочнике;
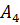 – студент найдет формулу в 4-ом справочнике.
– студент найдет формулу в 4-ом справочнике.
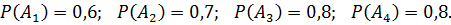
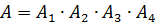
и и и
попарно незав.
По теореме умножения вероятностей независимых событий
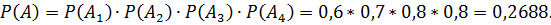
б) 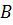 - студент найдёт её в первом и четвёртом справочниках (но не найдет во втором и не найдет в третьем)
- студент найдёт её в первом и четвёртом справочниках (но не найдет во втором и не найдет в третьем)
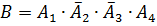
попарно незав.
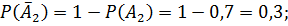
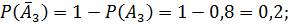
По теореме умножения вероятностей независимых событий
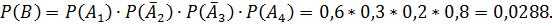
в) 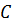 – студент найдет формулу в трёх справочниках
– студент найдет формулу в трёх справочниках
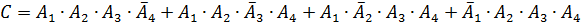
или или или
попарно несовместные
По теореме сложения вероятностей несовместных событий и теореме умножения вероятностей независимых событий
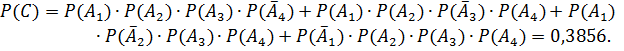
г) 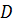 - он найдёт её хотя бы в одном справочнике
- он найдёт её хотя бы в одном справочнике
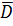 – не найдет ни в одном справочнике
– не найдет ни в одном справочнике
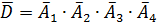
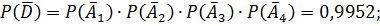
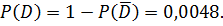
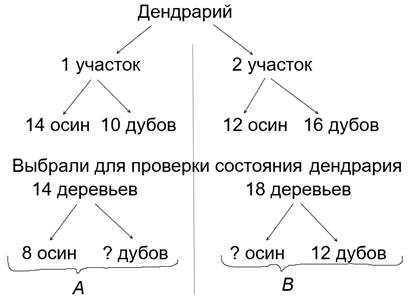
Задача № 3. Дендрарий разделен на 2 участка: в первом находятся 14 осин и 10 дубов, а во втором – 12 осин и 16 дубов. Для проверки состояния дендрария в первом участке выбрали 14 деревьев, а во втором – 18 деревьев. Какова вероятность, что в первом участке выбраны 8 осин, а во втором – 12 дубов?
Решение.
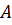 – в 1-м участке выбрали 14 деревьев: 8 осин, 6 дубов;
– в 1-м участке выбрали 14 деревьев: 8 осин, 6 дубов;
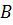 – во 2-м участке выбрали 18 деревьев: 6 осин, 12 дубов;
– во 2-м участке выбрали 18 деревьев: 6 осин, 12 дубов;
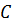 - в 1-м участке выбраны 8 осин, а во 2-ом – 12 дубов.
- в 1-м участке выбраны 8 осин, а во 2-ом – 12 дубов.
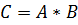
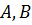 – независимые
– независимые
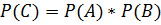
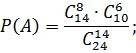
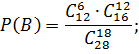
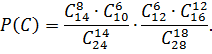
Задача № 4. При увеличении напряжения может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов; вероятности отказа элементов равны 0,1; 0,2; 0,3. Определить вероятность того, что разрыва цепи не произойдет.
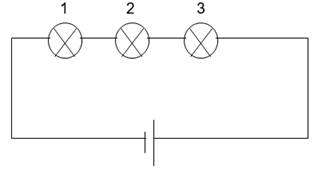
Решение.
Выписываем события:
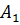 – отказ 1-го элемента;
– отказ 1-го элемента;
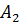 – отказ 2-го элемента;
– отказ 2-го элемента;
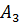 – отказ 3-го элемента;
– отказ 3-го элемента;
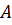 – разрыва цепи не произойдет
– разрыва цепи не произойдет
Разрыва цепи не произойдет только в том случае, если все элементы не откажут:
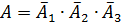
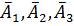 – попарно независимые события. По теореме умножения для независимых событий
– попарно независимые события. По теореме умножения для независимых событий
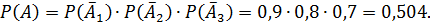
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|