
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение неравенств методом интервалов
ИС1-20-ОТ – 06.11.2020, 07.11.2020
Решение неравенств методом интервалов
№ 1. Решить неравенство
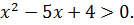
Выписываем корни неравенства – те 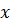 , при которых выражение равно 0:
, при которых выражение равно 0:
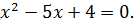
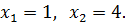
Наносим эти значения на числовую прямую в порядке возрастания. Так как неравенство строгое (>, без равенства), то эти точки «выкалываем».
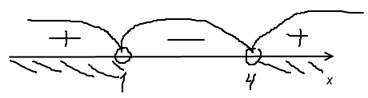
«Разбиваем» числовую прямую на интервалы, образованные этими точками. Поскольку перед старшей степенью положительное число +1, то выражение в крайнем правом интервале положительно (+). Дальше знаки чередуются. Знаки можно расставить и с помощью подстановки: к примеру, в крайнем правом интервале возьмем 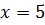 и подставим в выражение в неравенстве:
и подставим в выражение в неравенстве: 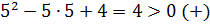 .
.
Поскольку знак неравенства больше (>), то выбираем интервалы с плюсом.
Ответ: 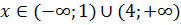 .
.
№ 2. Решить неравенство 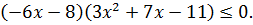
Находим корни неравенства:
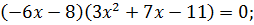
Произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0:
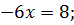
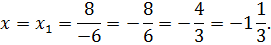
| 
| 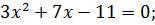
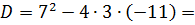
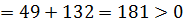
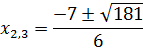
|
Старшие коэффициенты перед x в каждом множителе имеют знаки -+ ; если умножить отрицательное и положительное число, то получится отрицательное число, поэтому в крайнем правом интервале будет отрицательный знак. Знак неравенства нестрогий, поэтому точки выделяются.
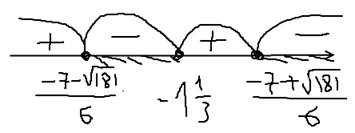
Выбираем интервалы с “-“, так как выражение меньше 0.
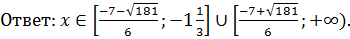
№ 3. Решить неравенство: 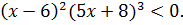
Корни неравенства: 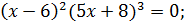

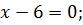
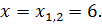
| 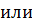
| 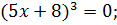
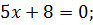
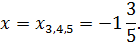
|
Так как в первом уравнении стоит в показателе степени 2, то корень 6 кратности 2. Так как во втором уравнении стоит в показателе степени 3, то корень 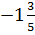 кратности 3. Если корень четной кратности, то на числовой прямой знак повторяется(!). В противном случае меняется.
кратности 3. Если корень четной кратности, то на числовой прямой знак повторяется(!). В противном случае меняется.
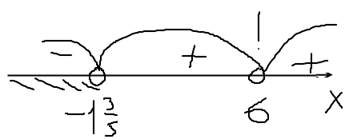
Ответ: 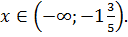
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|