
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Иррациональные уравнения
Задание по математике для 1 курсов всех отделений
Тема: Иррациональные уравнения
1. Актуализация знаний.
2. Дайте определение корня п-ой степени, приведите примеры.
3. Назовите свойства корней.
4. Объясните решение и запишите следующие примеры:
1) 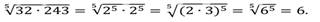
2) 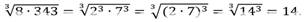
3) 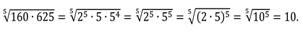
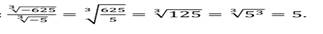 4)
4) 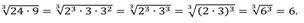
5)
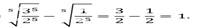
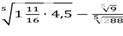 6)
6) 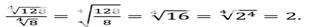
7) = 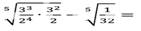
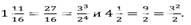
2. Изучение нового материала
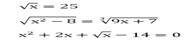 Иррациональное уравнение – это уравнение, в котором переменная содержится под знаком корня.
Иррациональное уравнение – это уравнение, в котором переменная содержится под знаком корня.
Примеры иррациональных уравнений:
Основные методы решения иррациональных уравнений:
1. Метод возведения обеих частей уравнений в одну и ту же степень;
При возведении обеих частей иррациональных уравнений в четную степень возможно появление посторонних корней. Поэтому при использовании этого метода необходимо провести проверку
2. Метод введения новых переменных.
Алгоритм решения уравнений
Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной.
При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.
Иногда удобнее решать иррациональные уравнения, определив область допустимых значений неизвестного и используя равносильные переходы.
Решить уравнения:
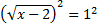 1)
1) 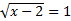 В левой части стоит корень второй степени, чтобы избавиться от него, возведём обе части уравнения во вторую степень:
В левой части стоит корень второй степени, чтобы избавиться от него, возведём обе части уравнения во вторую степень:
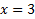
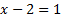
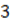 Выполним проверку. Подставим найденный корень в исходное уравнение.
Выполним проверку. Подставим найденный корень в исходное уравнение.
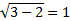
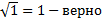 Значит, корень 3 подходит Ответ: х= 3
Значит, корень 3 подходит Ответ: х= 3
2) 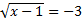 В левой части стоит корень второй степени, чтобы избавиться от него, возведём обе части уравнения во вторую степень:
В левой части стоит корень второй степени, чтобы избавиться от него, возведём обе части уравнения во вторую степень:
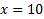 | |||||
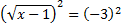 | |||||
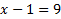 | |||||
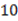 Выполним проверку. Подставим найденный корень в исходное уравнение:
Выполним проверку. Подставим найденный корень в исходное уравнение:
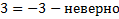
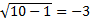 Значит, число
Значит, число 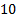 не является корнем исходного уравнения.
не является корнем исходного уравнения.
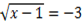 Ответ: уравнение решений не имеет.
Ответ: уравнение решений не имеет.
На самом деле то, что уравнение не имеет решений, можно сказать сразу. Так как в левой части стоит квадратный корень, а он принимает только неотрицательные значения, а в правой части стоит 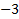 – отрицательное число.
– отрицательное число.
3) 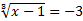 , В левой части стоит корень третьей степени, чтобы избавиться от него, возведём обе части уравнения в третью степень:
, В левой части стоит корень третьей степени, чтобы избавиться от него, возведём обе части уравнения в третью степень:
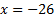
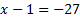
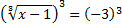 Ответ: х= - 26
Ответ: х= - 26
Так как степень корня нечётная, проверку можно не выполнять.
4) 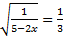 В левой части стоит корень второй степени, чтобы избавиться от него, возведём обе части уравнения во вторую степень:
В левой части стоит корень второй степени, чтобы избавиться от него, возведём обе части уравнения во вторую степень:
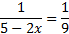
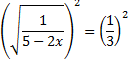
Воспользуемся правилом пропорции (умножаем числитель и знаменатель крест-на-крест)
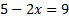
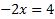
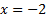 Выполним проверку. Подставим найденный корень
Выполним проверку. Подставим найденный корень 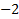 в исходное уравнение:
в исходное уравнение:
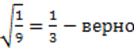
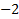
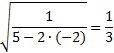
Значит, число является корнем исходного уравнения. Ответ: х= 2
5. 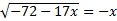 Возводим обе части уравнения в квадрат:
Возводим обе части уравнения в квадрат:
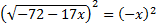
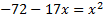
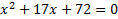
Получили квадратное уравнение. Решим его:
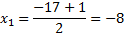
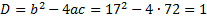
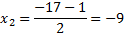
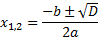
Выполним проверку: 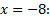
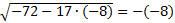
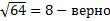 .
. 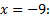
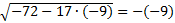
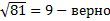 Ответ:
Ответ: 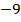 ;
; 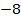
 6)
6)
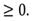
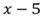
|
 Ответ: х= 8
Ответ: х= 8
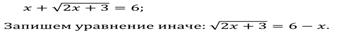 7)
7)
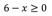
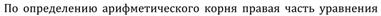
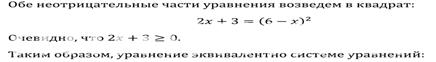
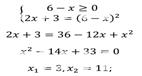 |
 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|