
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Приложение определенных интегралов
09.11.2020 ЕН.01 Математика С-21
Ход работы:
1. В тетради по математике записать тему и дату занятия.
2. Повторите тему I от 10.11.2020
3. На основании данных таблицы решить №1 (рисунки перечерчивать схематично).
4. Изучить (одновременно с примером 1) алгоритм нахождения площади фигуры. Пример1 записать в тетрадь.
5. Решить самостоятельно №2 в тетради по аналогии с примером 1.
Выполненную работу сдаём на проверку до 11.11.2020
Критерии оценки:
«3» - выполнены пункты 1, 4.
«4» - выполнены пункты 1, 3, 4.
«5» - выполнены пункты 1, 3, 4, 5,
(!) Если работа сдана позднее указанного срока, то она оценивается на «3».
Тема: Приложение определенных интегралов
Определенный интеграл широко используется при вычислениях различных геометрических и физических величин: вычисление площади плоских фигур, вычисление объемов тел вращения, вычисление длины дуги, вычисление пути, пройденного телом, вычисление работы силы.
I. Вычисление площадей плоских фигур.
Фигура, ограниченная кривой y = f(x), осью 0х, прямыми х = а, х = в называется криволинейной трапецией.
| Расположение графиков функций на координатной плоскости | Формула для вычисления площади | ||
| 1) | | Криволинейная трапеция ограничена осью Ох и лежит над ней. |

|
| 2) | | Криволинейная трапеция ограничена осью Ох и лежит под ней. |
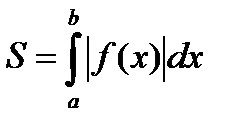
|
| 3) | |
Фигура ограничена двумя кривыми 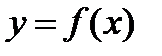 и и 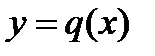
|
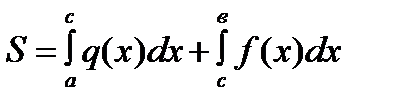
|
| 4) | | Фигура не ограничена осью Ох | 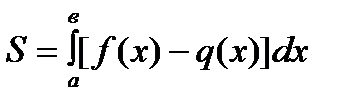
|
№1. Используя данные из таблицы, для каждого рисунка напишите формулу, по которой вычисляется площадь заштрихованной фигуры.
1) 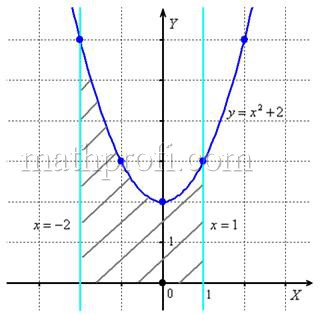 2)
2) 3)
4)
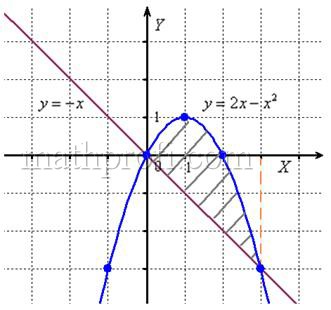
Алгоритм нахождения площади фигуры:
1. Построить на одной координатной плоскости графики данных функций.
2. Заштриховать фигуру, ограниченную построенными линиями.
3. Найти точки, ограничивающие фигуру справа и слева.
4. Найти площадь фигуры по соответствующей формуле.
Пример 1. Найти площадь фигуры, ограниченную линиями: 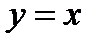 и
и 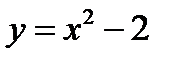
Решение: Построим графики данных функций
| |
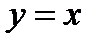 - прямая
- прямая
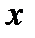
| -1 | ||
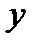
| -1 |
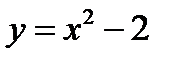 - парабола, ветви вверх
- парабола, ветви вверх
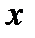
| -1 | -2 | |||
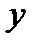
| -2 | -1 | -1 |
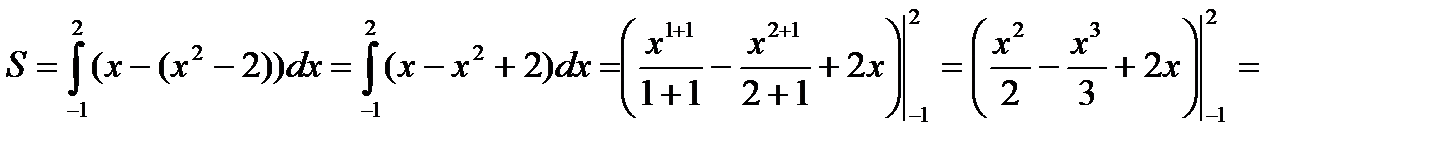
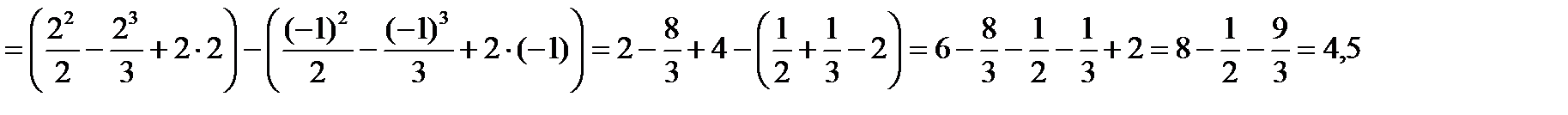
№2.Найти площадь фигуры, ограниченную линиями: 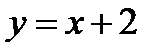 и
и 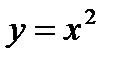
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|