
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОУД.04 Математика (2 пары) группа ПС-11 11.11.2020
ОУД.04 Математика (2 пары) группа ПС-11 11.11.2020
Внимание!
1. Высылаем на проверку11 ноября до 13.00 часовтеорию по теме 7 с примером 1.
«5» - выполнено разборчиво, по инструкции.
«4» - выполнено по инструкции с некоторыми замечаниями.
«3» - выполнено позднее указанного срока.
«2» - не выполнено.
2. Высылаем из ТТ решения заданий по темам 5, 6 и 7 до 13 ноября.
«5» - 10-12 баллов и в указанный срок
«4» - 8-9 баллов и в указанный срок
«3» - 5-7 баллов или не в указанный срок
Тема 7 Основные тригонометрические формулы
Так как все тригонометрические функции рассматриваются на окружности, значит они между собой взаимосвязаны, и эта связь выражается с помощью формул.
Равенство, которое показывает зависимость синуса и косинуса называется основным тригонометрическим тождеством:
sin²α + cos²α = 1 (1)
Из равенства (1) можно выразить sinα через cosα и наоборот:
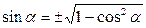 (2)
(2) 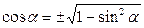 (3)
(3)
В равенствах (2) и (3) знак перед корнем определяется знаком тригонометрической функции, стоящей в левой части этих формул, а именно, в формуле (2) – знаком синуса, а в формуле (3) – знаком косинуса.
Зависимость между тангенсом и котангенсом определяется формулой:
tgα · ctgα = 1 (4)
Из равенства (4) можно выразить tgα через ctgα и наоборот:
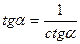 (5)
(5) 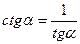 (6)
(6)
Формулы (5) и (6) показывают, что функции tgα и ctgα взаимно обратные.
Пример 1 Найдите значение каждой из тригонометрических функций, если
sinα=0,8 и 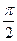 < α <
< α < 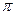
Решение: по формуле (3) находим cosα
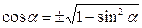 =
= 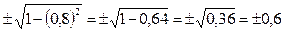 , но так как
, но так как
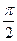 < α <
< α < 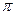 - это II четверть и в этой четверти cosα < 0, значит
- это II четверть и в этой четверти cosα < 0, значит 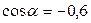
По определению (тема 3, формула 1) 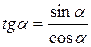 =
= 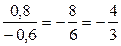 ,
,
а функция 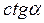 обратная функции
обратная функции 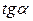 , значит
, значит 
 .
.
Ответ: 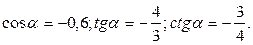
Выполните задание самостоятельно (в другой тетради):
№1 Найдите значение каждой из тригонометрических функций, если
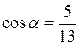 и
и 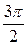 < α <
< α < 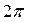 .
.
Ход решения:
1) Найти sinα по формуле (2).
2) Определите знак sinα (+ или -), учитывая четверть данного угла α.
3) Найти tgα по формуле 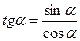 и сtgα по формуле (6).
и сtgα по формуле (6).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|