
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОУД.04 Математика группа ПС-11 09.11.2020
ОУД.04 Математика группа ПС-11 09.11.2020
Рекомендации:
- не забывайте изучать Тему 6 по инструкции от 02.11.2020;
- каждая следующая тема содержит в себе материал из ранее изученных тем, поэтому смотрите и повторяйте предыдущий материал;
- в обеих тетрадях ставим на полях дату занятия по расписанию.
Тема 6 Периодичность тригонометрических функций
Так как тригонометрические функции можно рассматривать на окружности, понятно, что окружность – замкнутая линия и по ней можно двигаться в любом направлении и выполнять бесконечное количество оборотов. Значит, с каждым следующим оборотом, мы будем попадать в те же самые точки, значения которых повторяются. Вращательное движение точки по окружности – процесс периодический. На основании этого можно сделать вывод, что все тригонометрические функции периодические или имеют период.
Функция f(x) называется периодической, если существует такое число Т≠0, что для любого х из области определения этой функции выполняется равенство f(x-T)=f(x)=f(x+T), число Т называется периодом функции f(x).
Периодическими функциями описываются многие физические процессы (колебание маятника, вращение планет, переменный ток и т.д.).
Наименьший положительный период синуса и косинуса равен 2π или 360°, а тангенса и котангенса π или 180°.
Свойство периодичности тригонометрических функций можно выразить формулами, где 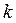 , которое задаёт целое число поворотов:
, которое задаёт целое число поворотов:
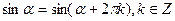
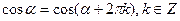
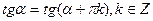
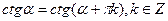
Так как тригонометрические функции периодические, то вычисление их значений для любого большого положительного аргумента можно свести к вычислению их значений на промежутке от 0 до 2π, а для тангенса и котангенса на промежутке от 0 до π путём исключения количества целых оборотов больше чем 360°. 1 круг – 360°, 2 круга – 720°, 3 круга – 1080° и т.д., 10 кругов – 3600°.
Пример 1 Вычислить: а) cos 765°; б) tg  .
.
Решение: Значения углов для каждой данной тригонометрической функции выходят за рамки одного круга (т.е. больше 360°), поэтому надо угол уменьшить до табличного значения, т.е. меньше, чем 360°. Для упрощения работы (под буквой б)) можно угол из радианной меры перевести в градусную (Тема 1).
а) cos 765° = cos (765°-360°) = cos 405° = cos (405°-360°) = cos 45° = 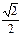
б) tg  = tg 855° = tg (855°- 360°) = tg 495° = tg (495°-180°) = tg 315° = -1
= tg 855° = tg (855°- 360°) = tg 495° = tg (495°-180°) = tg 315° = -1
Пример 2 Вычислить: cos 7230° - sin (-900°).
Решение: Сначала учитываем нечётность функции sin (Тема 5), а затем уменьшаем углы.
cos 7230° - sin (-900°) = cos 7230° + sin 900° = cos (7230°-3600°) + sin (900°-720°) =
= cos (7230°-3600°) + sin (900°-720°) = cos 3630° + sin 180° =
= cos (3630°- 3600°) + sin 180° = cos 30° + sin 180° = 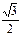 + 0 =
+ 0 = 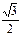
Выполните задание самостоятельно
№1 Вычислить: а) sin 3720°; б) 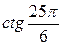 ; в)
; в) 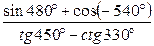
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|