
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОУД.04 Математика (2 пара) группа ПС-11 07.11.2020
ОУД.04 Математика (2 пара) группа ПС-11 07.11.2020
Рекомендации:
- не забывайте изучать Тему 5 по инструкции от 02.11.2020;
- каждая следующая тема содержит в себе материал из ранее изученных тем, поэтому смотрите и повторяйте предыдущий материал;
- в обеих тетрадях ставим на полях дату занятия по расписанию.
Тема 5 Четность и нечетность тригонометрических функций
Свойства четности и нечетности тригонометрических функций выражаются следующими формулами:
(1) sin(-α) = -sin α - нечётная функция
(2) cos(-α) = cos α - чётная функция
(3) tg(-α) = -tg α - нечётная функция
(4) ctg(-α) = -ctg α - нечётная функция
Из данных формул можно сделать вывод, что функции синус, тангенс и котангенс являются нечетными, а функция косинус – четная.
Свойства четности или нечетности тригонометрических функций позволяет находить значения этих функций для отрицательных аргументов с помощью таблицы значений для положительных аргументов.
Пример 1 Вычислить 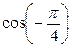
Решение: Сначала пользуемся формулой (2), т.е. чётностью функции cos, а затем значение cos смотрим по таблице (тема 4)
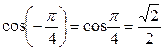
Пример 2 Вычислить 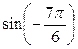
Решение: Сначала пользуемся формулой (1), т.е. нечётностью функции sin – знак минус переходит вперёд, а затем значение sin смотрим по таблице (тема 4)
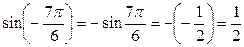
Пример 3 Вычислить 
Решение: Сначала пользуемся формулой (3), т.е. нечётностью функции tg – знак минус переходит вперёд, а затем значение tg смотрим по таблице (тема 4)
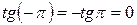
Пример 4 Вычислить 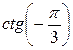
Решение: Сначала пользуемся формулой (4), т.е. нечётностью функции ctg – знак минус переходит вперёд, а затем значение ctg смотрим по таблице (тема 4)
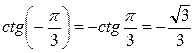
Пример 5 Вычислить 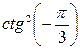
Решение: Обращаем внимание на степень 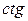 – она чётная, значит по формуле (4) минус, переходящий вперёд, в квадрате даёт знак «+», а затем значение ctg смотрим по таблице (тема 4). Так поступаем с любой чётной степенью.
– она чётная, значит по формуле (4) минус, переходящий вперёд, в квадрате даёт знак «+», а затем значение ctg смотрим по таблице (тема 4). Так поступаем с любой чётной степенью.

Если степень нечётная, то формулы (1), (3), (4) остаются без изменения.
Пример 6 Вычислить: 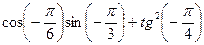
Решение:
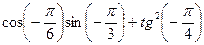 =
= 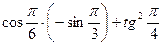 =
= 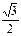 ∙(-
∙(- 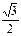 )+1² = -
)+1² = - 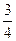 +1 =
+1 = 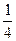
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|