Практическая работа № 8. Тема: Задание числовых последовательностей различными способами, вычисление членов последовательности.. Краткая теория. Практические задания

Практическая работа № 8

Тема: Задание числовых последовательностей различными способами, вычисление членов последовательности.

Цель: научиться записывать числовые последовательности различными способами, описывать их свойства.

Краткая теория

Функция у=f (n) натурального аргумента n (n=1; 2; 3; 4;...) называется числовой последовательностью.

Существуют следующие способы задания числовой последовательности:

1) Словесный способ. Представляет собой закономерность или правило расположения членов последовательности, описанный словами.

2) Аналитический способ. Последовательность задается формулой n-го члена: у_n=f(n). По этой формуле можно найти любой член последовательности.

3) Рекуррентный способ. Задается формула, по которой каждый следующий член находят через предыдущие члены. В случае рекуррентного способа задания функции всегда дополнительно задается один или несколько первых членов последовательности.

Числовую последовательность называют возрастающей, если ее члены возрастают (у_n+1>у_n) и убывающей, если ее члены убывают (у_n+1<у_n).

Возрастающая или убывающая числовые последовательности называются монотонными.

Практические задания

1. Задайте последовательность аналитически и найдите пять первых членов этой последовательности:

а) каждому натуральному числу ставится в соответствие противоположное ему число;

б) каждому натуральному числу ставится в соответствие квадратный корень из этого числа;

в) каждому натуральному числу ставится в соответствие половина его квадрата.

2. По заданной формуле n-го члена вычислите пять первых членов последовательности (y_n):

а) 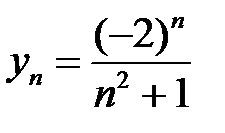; б) .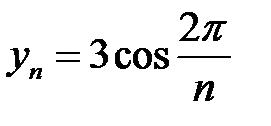

3. Является ли последовательность 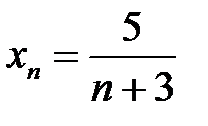ограниченной?

4. Является ли последовательность убывающей или возрастающей?

12 Следующая ⇒