Хелпикс

Главная

Контакты

Случайная статья



Практическая работа № 5. где Р = 0,845 + 0,005*Сн. где Р = 0,845 + 0,005*Сн



Практическая работа № 5

тема: «Организация выборочного наблюдения»

 

Задание 1.В городе проживает N = 2 200 семей. Определить размер выборки при условии, что предельная ошибка выборочной средней (Δ) не должна превышать 0,8 семьи с вероятностью Р и при среднем квадратическом отклонении σ = 2,0 семьи. Наблюдение будет проводиться по схеме бесповторной случайной выборки.

где Р = 0,845 + 0,005*Сн

Задание 2.По данным бесповторного выборочного наблюдения N = 10 000 малых предприятий предельная ошибка выборочной средней доли высококвалифицированных специалистов составилаΔ = 0,182. Объем выборки составил n = 50. Средняя доля составила ω. Определить достоверность предельной ошибки средней.

где ω = 0,2 + 0,005*Сн

Задание 3.Из 20 000 электроламп в порядке случайного бесповторного отбора взято 400 шт. и проведено испытание продолжительности горения. Оказалось, что средняя продолжи­тельность горения ламп в выборке ( 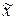) равно10 000 часов, а среднее квадратическое отклонение σ = 500 часов. С вероятностью Р определите, в каких пределах заключена средняя продолжительность горения электроламп.

где Р = 0,845 + 0,005*Сн

Задание 4.Статистическое управление города планирует проведение выбороч­ного обследо­вания банков для оценки среднегодового уровня оплаты труда банковских сотрудников. Известно, что максимальный среднегодовой уровень оплаты труда работников таких учреждений составляет Хmax = 740 000 руб., а минимальный уровень Хmin = 260 000 руб. Определить объем выборочной совокупности, обеспечив достоверность Р и предельную ошибку Δ = 0,01. Наблюдение будет проводиться по схеме повторной случайной выборки.

где Р = 0,845 + 0,005*Сн

Задание 5. При выборочном обследовании 46% студентов установлено, что доля студентов, имеющих трудовой стаж, составила ω. Определить среднюю ошибку выборки для доли, если известно, что в ВУЗе обучается N = 8 000 студентов. Отбор в выборку производился бесповторным способом.

где ω = 0,2 + 0,005*Сн
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.