
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 17. Тема: Вычисление определенных интегралов методом подстановки и по частям
Практическая работа № 17
Тема: "Вычисление определенных интегралов методом подстановки и по частям"
Цель работы: закрепление практических навыков вычисления определённых интегралов.
Ход работы:
1.Краткое содержание теоретического материала.
Определенный интеграл вычисляется по формуле Ньютона-Лейбница:
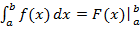 = F(a)-F(b)
= F(a)-F(b)
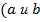 - соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
- соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
Основные свойства определенного интеграла:
1. При перестановке пределов интегрирования изменяется знак интеграла:

2. Отрезок интегрирования можно разбивать на части:
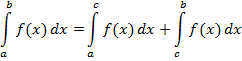
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов.
4. Постоянный множитель можно выносить за знак интеграла.
Пример 1.
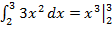 =
= 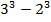 =27-8=19.
=27-8=19.
Вычисления определённого интеграла методом введения новой переменной.
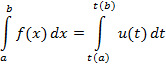
Пример 2.
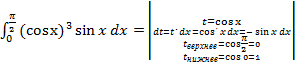 =
= 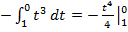 =
= 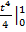 =
= 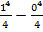 =
= 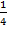
Пример 3.
 = -
= - 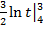 =-
=- 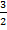 (
( 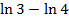 )=-
)=- 
Вычисление определенного интеграла по частям:
Используем формулу:
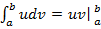 -
- 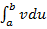
Пример 4.
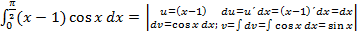 =
= 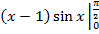 -
- 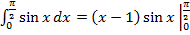 +
+ 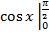 =(
=( 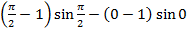 )+
)+ 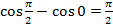 -1-1=
-1-1=  -2;
-2;
Пример 5.
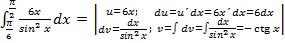 =-6xctgx
=-6xctgx  +
+ 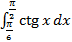 =-6·
=-6· 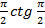 -6·
-6·  +ln|sinx|
+ln|sinx| 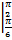 =π
=π 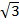 + ln|sin
+ ln|sin  |- ln|sin
|- ln|sin  |= π
|= π 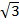 + ln1- ln
+ ln1- ln  = π
= π 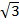 + 0+ln2= π
+ 0+ln2= π 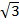 +ln2
+ln2
2.Выполнить самостоятельно:
Вычислить определенный интеграл.
| Вариант 1 | Вариант 2 |
1. 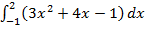
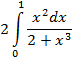 3
3  4
4 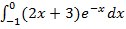
| 1. 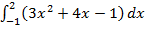 2
2 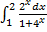 3
3 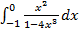 4
4 
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|