Практическая работа №15. Решение.

Практическая работа №15

Расчет элементов на устойчивость

Любая конструкция под воздействием приложенных к ней нагрузок деформируется. В результате деформации возникают внутренние напряжения, и любом сечении конструкции уравновешивает внешние силы, действующие по одну сторону от сечения.

Форму, которую конструкция приобретает в результате деформации, принято называть формой равновесия в деформированном состоянии. Эта форма может:

- устойчивой,

- неустойчивой

- безразличной по отношению к дополнительным воздействиям.

Стержни теряют устойчивость при действии нагрузок, направленных вдоль оси и вызывающих сжатие. Исходной формой равновесия при этом является прямолинейная, а смежной, соответствующей потере устойчивости, - криволинейная (изгибная). Совместное действие продольных и поперечных нагрузок приводит к так называемому продольно-поперечному изгибу, при котором существенный рост перемещений и напряжений может происходить при нагрузках, существенно меньших критических. Это определяет важность расчетов на продольно-поперечный изгиб.

Дано. Определить критическую нагрузку для сжатого стального стержня, имеющего прямоугольное поперечное сечение 46см. Концы стержня шарнирно закреплены. Длина стержня l = 0,8 м.

Решение.

Вычисляем минимальный радиус инерции поперечного сечения стержня:

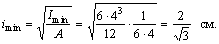
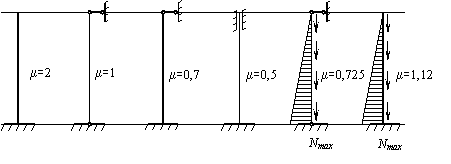
Согласно рисунку принимаем

Находим значение гибкости сжатого стержня:

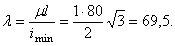
Так как 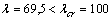, то для вычисления критического напряжения 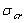используем формулу Ясинского 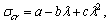предварительно выписав из таблицы (справочные данные) коэффициенты а = 310 МПа, в = 1,14 МПа, с = 0:

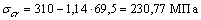
и тогда F_cr =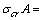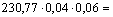0,55 мН = 550 кН.