
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа№6. Тема: Решение показательных уравнений и неравенств.. Показательные уравнения. Решение показательных неравенств
Практическая работа№6
Тема: Решение показательных уравнений и неравенств.
Цель работы: Овладение основными способами решения показательных уравнений и неравенств.
Задание:
Решить уравнение:
| 1. | 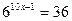
| 4. | 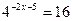
|
| 2. | 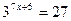
| 5. | 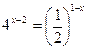
|
| 3. | 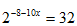
| 6. | 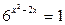
|
Решить уравнение:
| 7. | 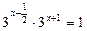
| 10. | 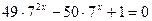
|
| 8. | 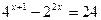
| 11. | 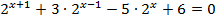
|
| 9. | 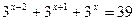
| 12. | 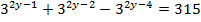
|
Решить неравенство:
| 13. | 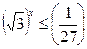
| 16. | 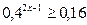
|
| 14. | 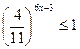
| 17. | 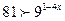
|
| 15. | 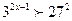
| 18. | 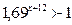
|
Решить неравенство:
| 19. | 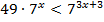
| 22. | 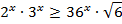
|
| 20. | 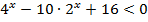
| 23. | 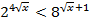
|
| 21. | 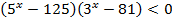
| 24. | 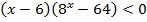
|
Найти область определения функции:
| 25. | 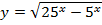
| 28. | 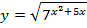
|
| 26. | 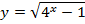
| 29. | 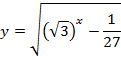
|
| 27. | 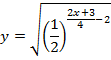
| 30. | 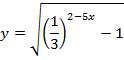
|
Пояснение к работе:
Показательные уравнения
Простейшие показательные уравнения имеют вид: 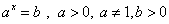 .
.
Уравнение 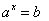 при
при 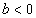 и при
и при 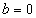 корней не имеет, так как показательная функция всегда положительна.
корней не имеет, так как показательная функция всегда положительна.
Если в уравнении присутствуют показательные функции с разными основаниями, можно попытаться привести их к одному и тому же основанию. То же относится и к логарифмическим уравнениям.
-
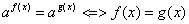 при
при 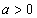 ,
, 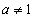 ;
; -
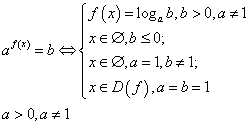 .
.
Решение показательных неравенств
При решении показательных неравенств вида 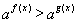 следует помнить, что показательная функция
следует помнить, что показательная функция 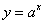 возрастает при
возрастает при 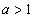 и убывает при
и убывает при 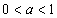 . Значит, в случае, когда
. Значит, в случае, когда 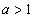 , от неравенства
, от неравенства 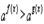 следует переходить к неравенству того же смысла
следует переходить к неравенству того же смысла 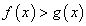 . В случае же, когда
. В случае же, когда 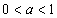 , от неравенства
, от неравенства 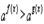 следует переходить к неравенству противоположного смысла
следует переходить к неравенству противоположного смысла 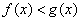 .
.
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
2. Цель работы
3. Задание
4. Выполненная практическая работа в соответствии с заданием
5. Ответы на контрольные вопросы
6. Вывод
Контрольные вопросы:
1) Дайте определение показательного уравнения.
2) Назовите способы решения показательных уравнений.
3) Запишите свойства степени с рациональным показателем.
4) Сформулируйте правило решения простейших показательных уравнений.
5) Запишите чему равна степень с отрицательным показателем.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|