
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рабочий лист.
Рабочий лист.
| Предмет | Математика |
| Группа | № 1 2 курс |
| Тема урока | Векторы. Действия с векторами заданными координатами. |
| ФИО преподавателя | Тимиршина Алия Мунзиловна |
| Где находится задание: | |
| Учебник | М.И. Башмаков Математика, задачник, 2017г |
| Ссылка | http://www.belgtis.ru/images/obuch/pm/MatematikaZadachnikBashmakov.pdf |
| Сроки выполнения задания | 07.09.2020 до 17:00 |
| Как выполнять задание | Написать конспект и выполнить домашнее задание. |
| Домашняя работа | По задачнику М.И. Башмакова на стр.102 №5.6, на стр.114 №5.45 |
| Обратная связь | Выполненные работы отправить личным сообщением ВК |
| Как узнать отметку о выполненном задании | Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК. |
Тема: Векторы. Действия с векторами заданными координатами.
Длина (модуль) вектора 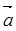 обозначается
обозначается 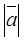 и определяется по формуле:
и определяется по формуле:

|
Вектор 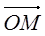 , начало которого находится в начале координат, а конец – в точке М(x;y;z) называют радиусом – вектором точки М и обозначают
, начало которого находится в начале координат, а конец – в точке М(x;y;z) называют радиусом – вектором точки М и обозначают 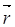 (М) или просто
(М) или просто 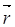 . Так как его координаты совпадают с координатами точки М, то его разложение по ортам имеет вид:
. Так как его координаты совпадают с координатами точки М, то его разложение по ортам имеет вид:
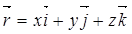
|
Вектор 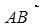 , имеющий начало в точке А( х1; y1; z1) и конец в точке В(х2; y2; z2) может быть записан в виде
, имеющий начало в точке А( х1; y1; z1) и конец в точке В(х2; y2; z2) может быть записан в виде 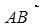 =
= 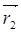 -
- 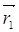 , где
, где 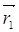 - радиус- вектор точки А,
- радиус- вектор точки А, 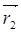 - радиус – вектор точки В.Поэтому разложение вектора
- радиус – вектор точки В.Поэтому разложение вектора 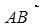 по ортам имеет вид:
по ортам имеет вид:
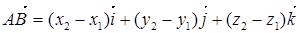
|
Его длина совпадает с расстоянием между точками А и В:
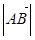 = = 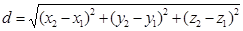
|
Координаты вектора
Числа x, y и z называются координатами вектора 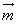 в данном базисе. В этом случае пишут:
в данном базисе. В этом случае пишут:
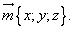
Действия над векторами, заданными своими координатами

| Сложение | Вычитание | Умножение |
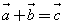 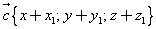 При сложении векторов их соответстветственные координаты складываются.
При сложении векторов их соответстветственные координаты складываются.
| 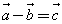  При вычитании векторов их соответстветственные координаты вычитаются.
При вычитании векторов их соответстветственные координаты вычитаются.
| 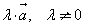 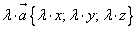 При умножении вектора на число все его координаты умножаются на это число.
При умножении вектора на число все его координаты умножаются на это число.
|
IV. Закрепление нового материала:
Задача № 1
Точка К – середина отрезка АВ. Найдите длину отрезка АВ, если известны координаты точек А и К.
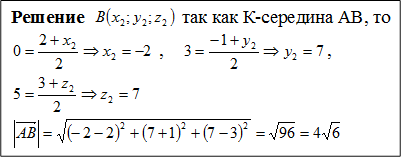

Задача № 2
От точки Р, координаты которой известны, отложили вектор с концом в точке Q, длиной 3 и сонаправленный вектору с координатами (4; -4; 2). Найдите координаты точки Q.


Задача № 3
Даны координаты двух векторов. Найдите длину вектора, который является линейной комбинацией исходных векторов. 

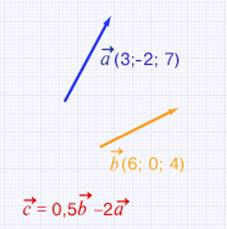
Задача №4 Найти длину вектора 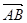 , если
, если 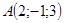 и
и 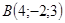
Решение:
 и
и 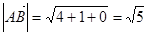
Задача №5 Найти длину вектора 
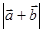 , если
, если 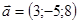 и
и 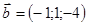
Решение:
Пусть  , тогда
, тогда 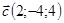 и
и 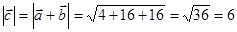
Задача №6. Найти длину вектора 
 , если
, если  и
и 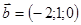
Решение:  и
и 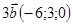 , пусть
, пусть  , тогда
, тогда 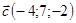


Домашнее задание: По задачнику М.И. Башмакова на стр.102 №5.6, на стр.114 №5.45
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|