
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Перпендикулярность плоскостей. Решение задач.
Тема: Перпендикулярность плоскостей. Решение задач.
Дата: 09.10.2020 г.
Группа: ПК-261
Студенты должны знать: понятие перпендикулярности плоскостей.
Студенты должны уметь:выполнять построение по условию задачи, решать задачи на применение теоремы о перпендикулярности плоскостей.
1.Актуализация знаний студентов
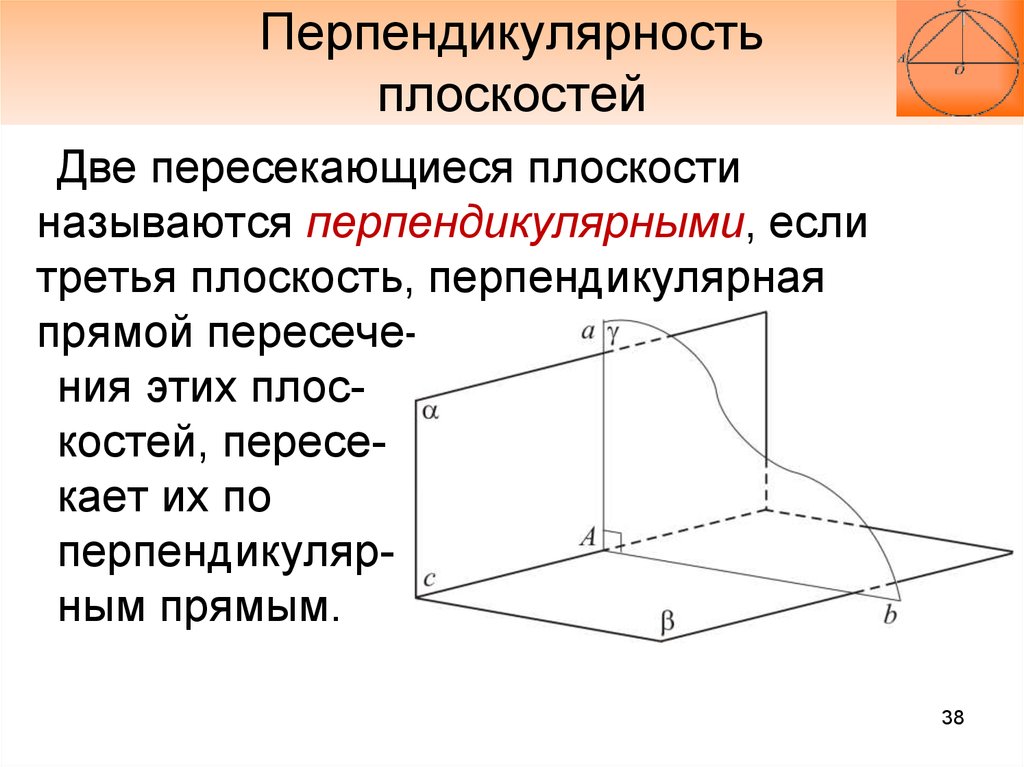
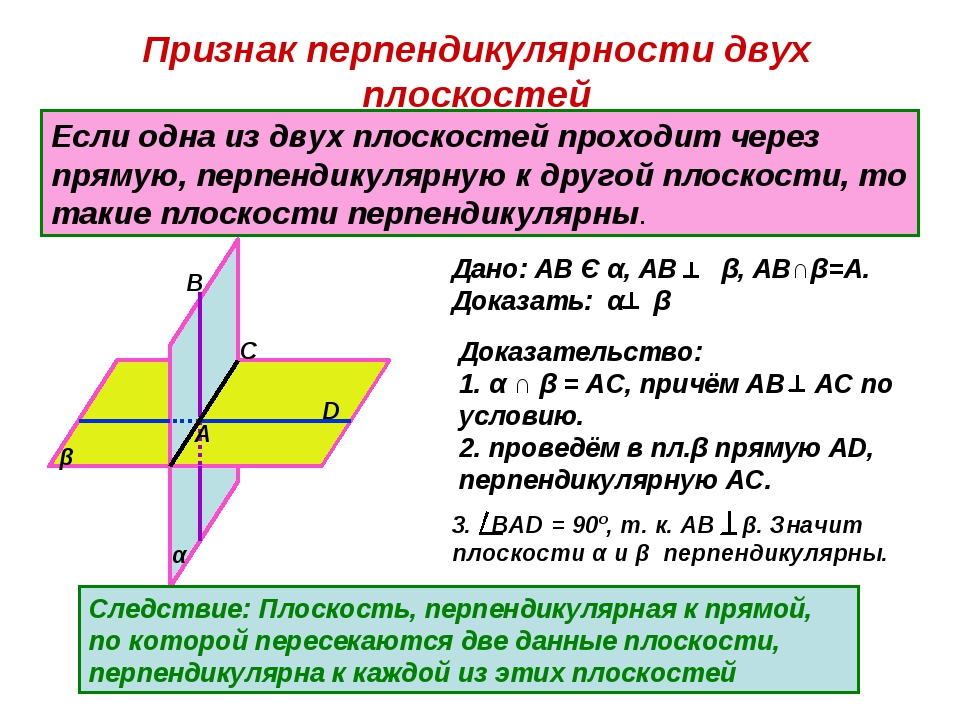
2.Решение задач.
1. Точки А и В лежат на ребре данного двугранного угла, равного 120°.
Отрезки АС и ВD проведены в разных гранях и перпендикулярны к ребру двугранного угла.
Найдите отрезок СD, если АВ = АС = ВD = а.
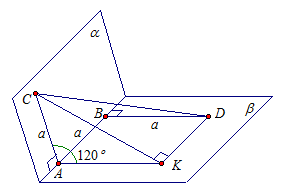 Дано: ∠САВD= 120°,
Дано: ∠САВD= 120°,
АС ⊥ АВ, АС ⊂ α,
BD ⊥ АВ, BD ⊂ β,
АВ = АС = ВD = а.
Найти: СD. Рис. 2
Решение: Здесь дан тупой двугранный угол, ∠САВD= 120°.
АВ – ребро двугранного угла, точка С лежит в одной полуплоскости, точка D лежит в другой полуплоскости. В одной полуплоскости проведена прямая АС, перпендикулярная АВ. В другой полуплоскости проведена прямая ВD, перпендикулярная АВ.
Проведем АК перпендикулярно АВ и DК параллельно АВ (рис. 2). Тогда угол САК – линейный угол двугранного угла, а значит, ∠САК = 120°.
Так как прямые АК и ВD перпендикулярны одной и той же прямой АВ, то прямые АК и ВD – параллельны. В четырехугольнике АКDВ противоположные стороны параллельны (AK∥BD, AB∥ DK), значит, АКВD– параллелограмм. Значит, АК=BD= а.
Рассмотрим треугольник АКС. Найдем 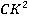 с помощью теоремы косинусов:
с помощью теоремы косинусов:
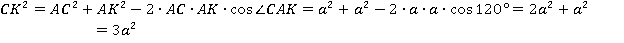
Прямая АВ перпендикулярна плоскости линейного угла (по свойству 1), значит, и параллельная ей прямая DК перпендикулярна плоскости линейного угла. А значит, прямая DК перпендикулярна прямой СК, лежащей в плоскости линейного угла, то есть угол СКD прямой.
Из прямоугольного треугольника СКD по теореме Пифагора находим гипотенузу СD.
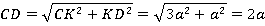
Ответ: 2а.
2.Найдите двугранный угол АВСD тетраэдра АВСD, если углы DАВ, DАС и АСВ прямые, АС = СВ = 5 DВ = 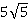 .
.
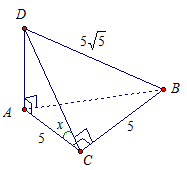 Дано: АВСD – тетраэдр.
Дано: АВСD – тетраэдр.
∠DАВ = ∠DАС = ∠АСВ = 90°.
АС = СВ = 5, DВ = 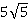 .
.
Найти: ∠ (АВСD) Рис. 6
Решение:
Прямая DA перпендикулярна пересекающимся прямым АВ и АС из плоскости АВС. Значит, прямая DA перпендикулярна плоскости АВС.
Тогда АС - это проекция DС на плоскость АВС. Проекция АС перпендикулярна прямой ВС из плоскости по условию, значит, и наклонная DС перпендикулярна прямой ВС (по теореме о трех перпендикулярах). Получаем, что угол АСD– линейный угол искомого двугранного угла.
Рассмотрим прямоугольный треугольник DСВ. Найдем DС по теореме Пифагора.
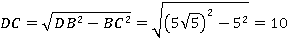
Рассмотрим прямоугольный треугольник АСD. Выразим косинус угла АСD.
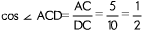 .
.
Тогда 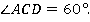
Ответ: 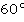 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|