
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Числовые ряды с произвольными членами.
Лекция от 05.11.
Числовые ряды с произвольными членами.
1)Знакочередующийся ряд. Признак Лейбница.
Этот вопрос изложен в разделе 10.5 пособия “Математический анализ” (файл Мат.ан.2013.pdf) – с. 95.
2) Абсолютная сходимость ряда. Связь обычной и абсолютной сходимости.
Этот вопрос изложен в начале следующего раздела того же пособия – раздел 10.6, с. 96 (до Замечания 10.3).
3)Ряды с комплексными членами.
Пусть 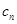 - последовательность комплексных чисел. Каждый член этой последовательности можно представить в алгебраической форме
- последовательность комплексных чисел. Каждый член этой последовательности можно представить в алгебраической форме 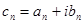 . Введем формально ряд
. Введем формально ряд 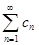 . Очевидно, частичная сумма этого ряда может быть записана в виде
. Очевидно, частичная сумма этого ряда может быть записана в виде 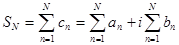 . Поэтому естественно определить
. Поэтому естественно определить 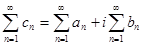 . Таким образом, сходимость ряда с комплексными членами равносильна сходимости двух рядов с вещественными членами – его вещественными и мнимыми частями.
. Таким образом, сходимость ряда с комплексными членами равносильна сходимости двух рядов с вещественными членами – его вещественными и мнимыми частями.
Для ряда с комплексными членами естественно сохраняется необходимое условие сходимости – стремление к 0 при  его общего члена. Действительно, комплексное число приближается к 0 тогда и только тогда, когда приближаются к 0 его вещественная и мнимая части.
его общего члена. Действительно, комплексное число приближается к 0 тогда и только тогда, когда приближаются к 0 его вещественная и мнимая части.
Так же, как в вещественном случае, вводится понятие абсолютной сходимости ряда с комплексными членами. Он называется абсолютно сходящимся, если сходится ряд с вещественными положительными членами 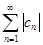 (напоминаю, что модуль комплексного числа
(напоминаю, что модуль комплексного числа 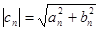 ).
).
Из абсолютной сходимости ряда с комплексными членами следует его сходимость. Действительно, если сходится 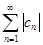 , то вследствие очевидных неравенств
, то вследствие очевидных неравенств 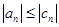 и
и 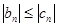 по признаку сравнения сходятся ряды
по признаку сравнения сходятся ряды 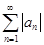 и
и 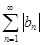 , то есть ряды
, то есть ряды 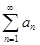 и
и 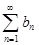 абсолютно сходятся, а значит сходятся. Это и означает, что сходится ряд
абсолютно сходятся, а значит сходятся. Это и означает, что сходится ряд 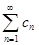 .
.
Пример. Рассмотрим ряд 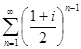 . Соответствующий ряд из модулей
. Соответствующий ряд из модулей 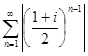 =
= 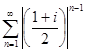 =
= 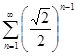 . Получилась сумма членов геометрической прогрессии со знаменателем <1, этот ряд сходится, поэтому исходный ряд абсолютно сходится, а значит сходится.
. Получилась сумма членов геометрической прогрессии со знаменателем <1, этот ряд сходится, поэтому исходный ряд абсолютно сходится, а значит сходится.
На самом деле, данный исходный ряд представляет собой сумму членов геометрической прогрессии с комплексным знаменателем, модуль которого <1. В этом случае остается справедливой формула суммы членов бесконечно убывающей геометрической прогрессии 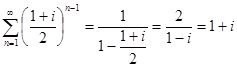 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|