
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Инструкция. Вариант 1
Инструкция
Проверочная работа по теме первообразная и интеграл составлена в четырёх вариантах и содержит задания, направленные на проверку знаний учащихся таблицы первообразных, основных формул и правил интегрирования. Данная работа содержит так же задания на применение интеграла. Каждый вариант содержит десять заданий. Первые три задания направлены на нахождение общего вида первообразной и первообразной, график, которой проходит через данную точку. Задания 4,5,8,9 позволяют проверить знания геометрического смысла первообразной. В заданиях 6 и 7 применяется формула Ньютона-Лейбница. Задание 10 позволяет проверить знания учащихся физического смысла производной. Каждое задание оценивается по трехбалльной системе.
Оценка 5 ставится, если учащийся набрал 28-30 баллов
оценка 4 ставится за 24-27 баллов
оценка 3 ставится за 18-23 балла, в остальных случаях ставится неудовлетворительно.
Вариант 1
| № | Задание | Ответ |
Найдите функцию f(x), для которой 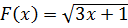 первообразной на первообразной на 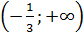 . .
| ||
Найдите первообразную 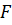 для функции f(x)=x4 на для функции f(x)=x4 на 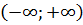 , график которой проходит через точку
М(-1;0,8) , график которой проходит через точку
М(-1;0,8)
| ||
Найдите общий вид первообразной для
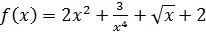 на на 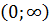
| ||
Найдите площадь фигуры, ограниченной линиями 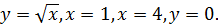
| ||
| Найдите площадь фигуры, ограниченной линиями y=x2 и x+y=6. | ||
Найдите 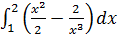
| ||
Вычислите 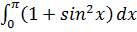
| ||
Используя геометрический смысл интеграла, найдите 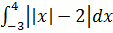 . .
| ||
Найдите площадь фигуры, ограниченной линиями y=cos2x, y=0, x=0, 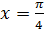 . .
| ||
Найдите путь, пройденный точкой за промежуток времени от t1=0 до t2 =4, если зависимость скорости тела v от времени t описывается уравнением
 (t - в секундах, v - в м/с). (t - в секундах, v - в м/с).
|
Вариант 2
| № | Задание | Ответ |
Найдите функцию f(x), для которой
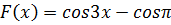 первообразной на первообразной на 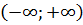 . .
| ||
Найдите первообразную 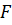 для функции f(x)=x2 на для функции f(x)=x2 на 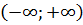 , график которой проходит через точку
М(-1;3) , график которой проходит через точку
М(-1;3)
| ||
Найдите общий вид первообразной для 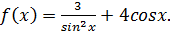
| ||
| Найдите площадь фигуры, ограниченной линиями y=x2 , x+y=6, y=0. | ||
Найдите площадь фигуры, ограниченной линиями 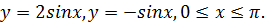
| ||
Вычислите интеграл 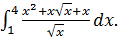
| ||
Вычислите 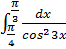
| ||
Используя геометрический смысл интеграла, найдите 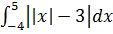 . .
| ||
Найдите площадь фигуры, которая ограничена графиком функции 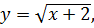 касательной к нему в точке с абсциссой x0=2 и прямой y=0. касательной к нему в точке с абсциссой x0=2 и прямой y=0.
| ||
Найдите закон движения точки, если скорость прямолинейного движения точки изменяется по закону 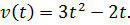
|
Вариант 3
| № | Задание | Ответ |
Найдите функцию f(x), для которой
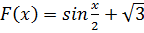 первообразной на первообразной на 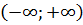 . .
| ||
Найдите первообразную 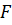 для функции f(x)= для функции f(x)= 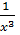 на на 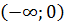 , график которой проходит через точку
М( , график которой проходит через точку
М( 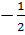 ;3). ;3).
| ||
Множество первообразных для функции
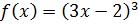 на на 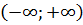 . .
| ||
Найдите площадь фигуры, ограниченной линиями 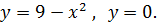
| ||
Найдите площадь фигуры, ограниченной линиями 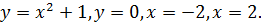
| ||
Вычислите интеграл 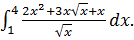
| ||
Вычислите интеграл 
| ||
Используя геометрический смысл интеграла, найдите 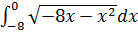 . .
| ||
Найдите площадь фигуры, которая ограничена графиком функции 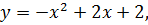 касательной к нему в точке с абсциссой x0=2 и прямой x=0. касательной к нему в точке с абсциссой x0=2 и прямой x=0.
| ||
Найдите скорость движения точки в момент t=3 c, если точка движется с ускорением, меняющимся по закону 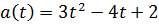 и в момент времени
t0=1с точка имела скорость v0 = 5 см/с. и в момент времени
t0=1с точка имела скорость v0 = 5 см/с.
|
Вариант 4
| № | Задание | Ответ |
Найдите функцию f(x), для которой
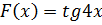 первообразной на первообразной на 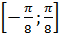 . .
| ||
Найдите первообразную 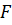 для функции f(x)= для функции f(x)= 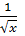 на на 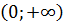 , график которой проходит через точку
М( , график которой проходит через точку
М( 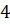 ; 5). ; 5).
| ||
Множество первообразных для функции
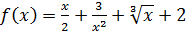 на на 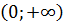 . .
| ||
Найдите площадь фигуры, ограниченной линиями 
| ||
Найдите площадь фигуры, ограниченной линиями 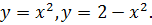
| ||
Вычислите интеграл 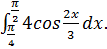
| ||
Вычислите интеграл 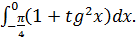
| ||
Найдите площадь фигуры, ограниченной линиями 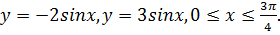
| ||
Используя геометрический смысл интеграла, найдите 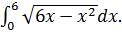
| ||
Найдите путь, пройденный точкой за промежуток времени от t1=1 до t2 =3, если зависимость скорости тела v от времени t описывается уравнением
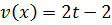 (t - в секундах, v - в м/с). (t - в секундах, v - в м/с).
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|