
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ИНСТРУКЦИОННАЯ КАРТА К ПРОВЕДЕНИЮ
Рассмотрено
на заседании цикловой комиссии гуманитарной и естественно- научной подготовки
Протокол №___от «___»____2020 г.
Председатель комиссии:
________________ С.Н. Лебеденко
ИНСТРУКЦИОННАЯ КАРТА К ПРОВЕДЕНИЮ
ПРАКТИЧЕСКОГО ЗАНЯТИЯ № 5
ПО ДИСЦИПЛИНЕ ОДП.01 МАТЕМАТИКА
Курс І Группа _________________
Тема занятия: Решение иррациональных уравнений и неравенств.
Целизанятия:
Учебная: Отработать умения и навыки решения иррациональных уравнений и неравенств.
Воспитательная: Обратить внимание студентов на приемы оформления, рациональную запись решения; достигать четкости и грамотности записи; воспитание чувства самоконтроля.
Междисциплинарная интеграция: математика, физика; общая электротехника.
Методическое обеспечение: Опорные конспекты по указанной теме; индивидуальные задания для отработки навыков решения иррациональных уравнений и неравенств.
Теоретическое обоснование работы.
Определение: Иррациональным называется уравнение, в котором неизвестное х находится под знаком корня.
Иррациональные уравнения часто получаются при решении различных задач. Решения иррациональных уравнений основано на следующем свойстве:
При возведении обеих частей уравнения в натуральную степень получается уравнение - следствие данного.
Определение: Область определения иррационального уравнения – это множество всех действительных значений переменной х, при которых одновременно имеют смысл выражения, входящие в уравнение.
Определение:Корни уравнения, не удовлетворяющие исходному уравнению, называются посторонними.
Примечание. При возведении уравнения в натуральную степень могут появиться посторонние корни, поэтому проверка необходима.
Если обе части уравнения f(x) = g(x) неотрицательны на множестве Х, то уравнение f(x) = g(x) равносильно уравнению (f(x))n = (g(x))n при n ϵ N
Иррациональным называется неравенство, в котором неизвестное х находится под знаком корня, при чем рассматриваются только арифметические корни, дан корень четной степени.
Задача 1. Решить неравенство 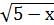 = 4
= 4
Найдем область определения неравенства, т. е. множество таких значений х, при которых имеют смысл обе части неравенства. Правая часть неравенства определена для всех значений переменной х, а левая – при 5-х ≥ 0, т.е. при х≤ 5. Следовательно, область определения неравенства - луч (-∞; 5].
При х≤ 5 обе части неравенства неотрицательны, поэтому при возведении обеих частей в квадрат получается равносильное ( на промежутке (-∞; 5]) неравенство 5 - х˂ 16.
Таким образом, указанное неравенство равносильно системе неравенств
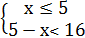
Решая эту систему, получаем -11˂ х ≤5
Рассуждения, приведенные при решении данной задачи, можно провести устно и сразу записать, что данное неравенство равносильно системе неравенств 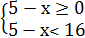
Содержание и ход работы:
1. Решить иррациональные уравнения и неравенства согласно варианту.
2. Ответить на вопросы самопроверки знаний.
3. Оформить отчет по практическому занятию.
Вариант № 1
І. Решить иррациональные уравнения следующими методами:
а) возведением обеих частей уравнения в степень и избавлением от радикалов:
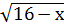 = х+4
= х+4
б) отделением квадратного корня:
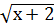 +
+ 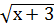 = 3
= 3
в) введением новой переменной:
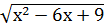 +
+ 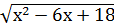 =9
=9
ІІ. Решить иррациональные неравенства следующими методами:
1. Основной уровень:
а) 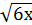 ˃ - 12;
˃ - 12;
б) 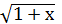 ≥
≥ 
2. Усложненный уровень
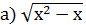 ˃
˃ 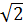 ;
;
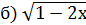 ˂·
˂· 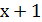
Вариант № 2
І. Решить иррациональные уравнения следующими методами:
а) возведением обеих частей уравнения в степень и избавлением от радикалов:
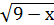 = х+3
= х+3
б) отделением квадратного корня:
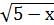 -
- 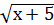 = 2
= 2
в) введением новой переменной:
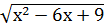 +
+ 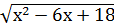 =9
=9
ІІ. Решить иррациональные неравенства следующими методами:
1. Основной уровень:
а) 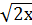 ≤ 2
≤ 2
б) 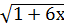 ˂ 9
˂ 9
2. Усложненный уровень
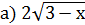 ˂
˂ 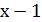 ;
;
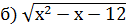 ˂·
˂· 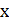
Вариант № 3
І. Решить иррациональные уравнения следующими методами:
а) возведением обеих частей уравнения в степень и избавлением от радикалов:
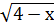 = х+2
= х+2
б) отделением квадратного корня:
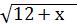 -
- 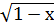 = 1
= 1
в) введением новой переменной:
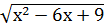 +
+ 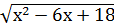 =9
=9
ІІ. Решить иррациональные неравенства следующими методами:
3. Основной уровень:
а) 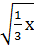 ˃ 9;
˃ 9;
б) 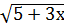 ˂ 7
˂ 7
4. Усложненный уровень
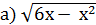 ˂
˂ 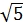 ;
;
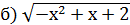 ˃ -1
˃ -1
Вариант №4
І. Решить иррациональные уравнения следующими методами:
а) возведением обеих частей уравнения в степень и избавлением от радикалов:
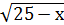 = х+5
= х+5
б) отделением квадратного корня:
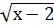 -
- 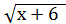 = 0
= 0
в) введением новой переменной:
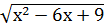 +
+ 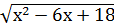 =9
=9
ІІ. Решить иррациональные неравенства следующими методами:
5. Основной уровень:
а) 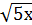 ˃ -9;
˃ -9;
б) 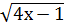 ˂ 3
˂ 3
6. Усложненный уровень
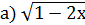 ˂
˂ 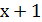 ;
;
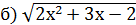 ˂·
˂· 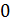
Вариант № 5
І. Решить иррациональные уравнения следующими методами:
а) возведением обеих частей уравнения в степень и избавлением от радикалов:
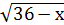 = х+6
= х+6
б) отделением квадратного корня:
1 - 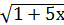 = х
= х
в) введением новой переменной:
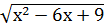 +
+ 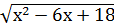 =9
=9
ІІ. Решить иррациональные неравенства следующими методами:
7. Основной уровень:
а) 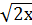 ˃ -3
˃ -3
б) 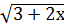 ˂ 4
˂ 4
8. Усложненный уровень
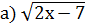 ˃
˃ 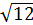 ;
;
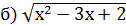 ˃ х+3
˃ х+3
Вариант № 6
І. Решить иррациональные уравнения следующими методами:
а) возведением обеих частей уравнения в степень и избавлением от радикалов:
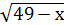 = х+7
= х+7
б) отделением квадратного корня:
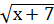 +
+ 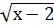 = 9
= 9
в) введением новой переменной:
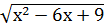 +
+ 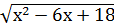 = 9
= 9
ІІ. Решить иррациональные неравенства одним из известных методов:
3. Основной уровень:
а) 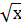 ˃ 2
˃ 2
б) 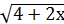 ˂ 1,5
˂ 1,5
4. Усложненный уровень
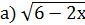 ˂
˂ 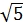 ;
;
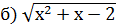 ˂·
˂· 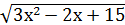
Вопросы для самопроверки:
1. Решить уравнения:
а) 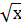 = 3; б)
= 3; б) 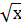 = 12; в)
= 12; в) 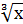 = 2; г)
= 2; г) 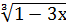 = 0
= 0
2. Выяснить с помощью графиков, сколько корней имеют уравнения:
а). 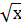 = 2 -
= 2 - 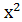 ;
;
б). 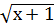 =
= 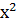 - 7
- 7
Использованная литература:
1. Ш.А. Алимов, Ю.М. Колягин и др. «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 кл. – М.: Просвещение, 2016. – 463 с.
2. Дидактические материалы по алгебре и началам анализа: кн.. для учащихся 10 кл. М.И.Шабунин, М.В.Ткачева, Н.Е.Федорова, Р.Г.Газарян. – М.: Просвещение, 2005
3. Дидактические материалы по алгебре и началам анализа: кн.. для учащихся 11 кл. М.И.Шабунин, М.В.Ткачева, Н.Е.Федорова, Р.Г.Газарян. – М.: Просвещение, 2005
4. Н. В. Богомолов «Практические занятия по математике »; М «Высшая школа», 1979.
ВЫВОДЫ ПО ВЫПОЛНЕННОЙ РАБОТЕ:________________________________________
СТУДЕНТ ДОЛЖЕН ЗНАТЬ:основные методы решения иррациональных уравнений и неравенств.
СТУДЕНТ ДОЛЖЕН УМЕТЬ:находить корни иррациональных уравнений и неравенств разными методами.
Преподаватель ___________________Л. А. Пузанко
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|