Задачи, которые приводят к понятию производной

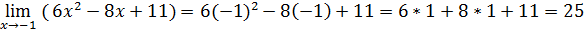
2.
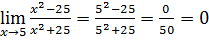
3.

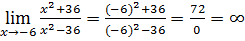
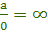только в теории пределов, после того, как мы уже подставили какое-то число вместо x.

Во всех других случаях говорим, что на 0 делить нельзя.

4. *

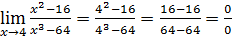При вычислении предела * мы получили в результате выражение , которое называется неопределённостью.

К неопределённостям также относятся выражения вида , , 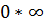, , 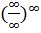и др.

Получение таких неопределённостей при вычислении предела означает, что данная точка для данной функции есть точка разрыва, но предел функции имеет место быть не в самой точке, а в её окрестности, поэтому существуют различные преобразования, в результате которых можно избавиться от неопределённости и вычислить предел.

Производная

Задачи, которые приводят к понятию производной

Задача 1

Мгновенная скорость прямолинейного движения материальной точки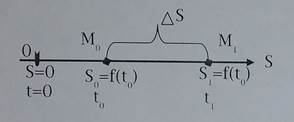

Материальная точка 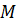двигается прямолинейно по закону 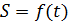и в момент времени 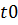заняла положение 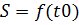. Найдём скорость точки в момент времени _..

Задача 2

Касательная к кривой

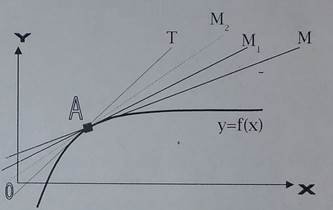
Касательной к графику функции 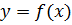в точке 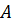называется предельное положение секущей 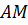, когда точка 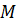, двигаясь по кривой графика 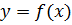, приближается к точке .

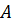Поставим задачу: провести секущую к графику функции 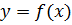в точке .

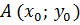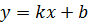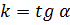Касательная – это прямая с общим уравнением , где , где – угол между прямой и положительным направлением оси OX. Т.е. наша задача сводится к нахождению k.

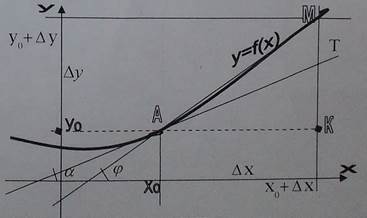
Решая обе задачи, поступали по одному и тому же плану:

1) независимой переменной x задавали приращение Δx и находили соответствующее приращение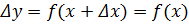

2) находили отношение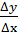

3) находили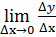

Т.к. такой план приходилось реализовывать неоднократно, было введено новое понятие:

Производной функции y=f(x) в точке x₀ является предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

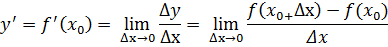
Замечание (что такое приращение):

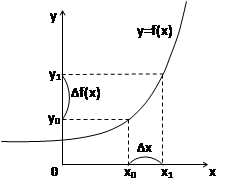(На данный момент лекции у нас были нарисованы только оси координат: x и y. График функции (кривая) ещё не был нарисован)

Функция – зависимость переменной y от переменной x, где x – это независимая переменная.

Поставим на оси x две точки: x₀ и x₁, причём на небольшом расстоянии друг от друга: приращение обычно < 1. Расстояние между этими точками и есть приращение.

Приращение аргумента (Δx):

Δx = x₁ – x₀ => x₁= x₀+ Δx

Понятие приращения функции тесно связано с таким понятием, как график функции. Построим какой-нибудь график (рисуем кривую). Проводим пунктирные линии от x₀ и x₁ до графика. Из точек их соприкосновения с графиком проводим пунктирные линии к оси y. Подписываем y₀и y₁.

Δf(x) – соответствующее приращение функции

Δf(x) = f(x₁) – f(x₀) = f (x+Δx) – f(x)