Лекция (занятие №26). Тема. Общая схема исследования функций с помощью производной: монотонность, экстремум, кривизна, ассимптоты; построение графиков.

Лекция (занятие №26)

Тема. Общая схема исследования функций с помощью производной: монотонность, экстремум, кривизна, ассимптоты; построение графиков.

1.Для уточнения поведения функции и формы ее графика рассмотрим некоторые вопросы, связанные с понятием кривизны кривой, а само понятие направления выпуклости.

Определение 1. Кривая называется выпуклой вниз на некотором интервале, если все ее точки лежат выше касательной, проведенной к этой кривой в любой точке этого интервала (Рис. 1).

Определение 2. Кривая называется выпуклой вверх на некотором интервале, если все ее точки лежат ниже касательной, проведенной к этой кривой в любой точке этого интервала (Рис. 2).

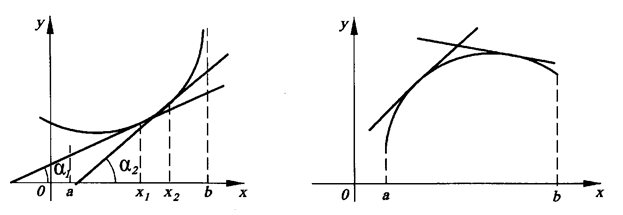
Теорема 1. Пусть функция f(x) определена и непрерывна вместе со своей производной f '(x) на некотором отрезке [ a,b] и имеет внутри этого отрезка конечную вторую производную f "(x) . Для выпуклости вниз функции f(x) на (a,b) необходимо и достаточно, чтобы выполнялось неравенство

f "(x) ≥ 0 ( на (a,b)). (1)

Аналогично, для выпуклости вверх функции получается условие

f "(x) ≤ 0 ( на (a,b)). (2)

Таким образом, требование f "(x) > 0 (f "(<0)) (3) заведомо обеспечивает строгую выпуклость вниз (вверх), потому что исключает возможность для функции f(x) быть линейной на каком бы то ни было интервале.

Определение 3. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпуклая вниз и вверх.

В точке перегиба касательная пересекает график функции, поскольку он переходит с одной стороны касательной на другую, то есть "перегибается" через ее (Рис. 3).

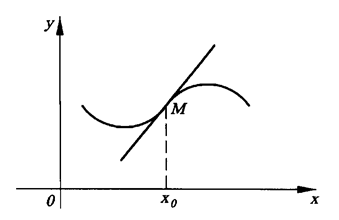
Теорема 2. (Необходимое условие). Если функция у = f (x) дважды дифференцируемая на интервале (a,b) и x0 (a,b) является точкой перегиба, то

f "(x) = 0 (4)

Действительно, так как функция дважды дифференцируемая, а справа и слева от точки перегиба вторая производная должна иметь разные знаки, то в точке (x=0 , f( x=0)) она должна быть равна нулю.

Замечание 1. Точки перегиба существуют и там, где вторая производная не существует.

Замечание 2. Если критическая точка дифференцируемой функции не является точкой экстремума, то эта точка есть точка перегиба.

Теорема 3. (Достаточное условие перегиба). Если вторая производная

f "(x) дважды дифференцируемой функции при переходе через некоторую точку x₀ меняет свой знак, то x₀ есть точка перегиба ее графика.

Итак, для того, чтобы изучить характер выпуклости графика функции

у = f(x) , необходимо исследовать знак производной в окрестности точки x₀, такой, что f "(x₀) = 0 или f "(x₀) не существует.

2. При исследовании функций и построении их графиков рекомендуется

использовать следующую схему:

1 °. Найти область определения функции.

2 °. Найти точки пересечения графика функции с осями координат.

3 °. Исследовать функцию на четность - нечетность.

4 °. Найти вертикальные асимптоты.

5 °. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты.

6 °. Найти экстремумы и интервалы монотонности функции.

7 °. Найти интервалы выпуклости функции и точки перегиба.

8 °. Найти некоторые дополнительные точки, уточняющие график.

9 °. Построить график функции.

Пример 1. Исследовать функцию 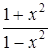и построить ее график.

Решение.

1 °. Область определения .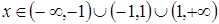

2 °. Точки пересечения с осями координат: f (0) = 1, то есть точка пересечения с осью ординат (0, l). Уравнение f (х) = 0 решений не имеет, следовательно, график функции не пересекает ось абсцисс.

3 °. Функция четная, поскольку f (-х) = f (х) . Ее график симметричен относительно оси ординат.

4 °. Вертикальные асимптоты могут пересекать ось абсцисс в точке х = ± 1. Найдем односторонние пределы: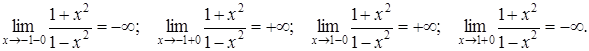

5 °. Поведение функции на бесконечности определяется границами

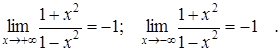
Это означает, что прямая у = -1 - горизонтальная асимптота.

6 °. Экстремумы и интервалы монотонности. Найдем у '(х):

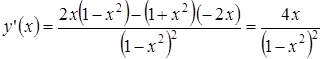
у '= 0 при х = 0 и у' не существует при х = ± 1.

Критической является точка х = 0 (поскольку точка х = ± 1 не входит в область определения функции).

f (x)				min
	-		-		+	+
x		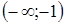-1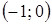

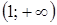
7 °. Интервалы выпуклости и точки перегиба. Найдем вторую производную:

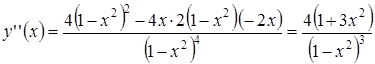
x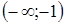
	-	+	-
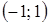
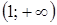
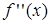
f (x)	Выпуклость вверх	Выпуклость вниз	Выпуклость вверх

f (x) выпуклость вверх выпуклость вниз, выпуклость вверх

Точек перегиба нет, так как уравнение не имеет действительных решений.

График функции имеет вид (Рис. 1)

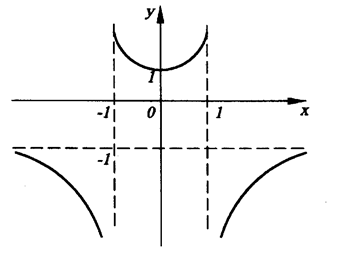
Рис. 1.

Пример 2. Построить график функции .

Решение.

1) Область определения функции - вся числовая прямая, кроме х = +1, x = -1.

2) f (х) - нечетная функция, так как f (-х) = - f (x). Поэтому для построения графика y = f (x) достаточно исследовать ее для х ≥ 0.

3) Функция непериодическая.

4) График функции пересекает оси координат только в точке (0; 0).

Точки x 1=-1, x 2 = 0 и x 3= 1 разбивают числовую прямую на четыре интервала: (-∞; -1), (-1; 0), (0; 1) и (1; +∞).

5) найдем знаки функции только в интервалах (0; 1) и (1; + ):

для всех ,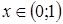

для всех .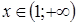

В силу нечетности данной функции имеем

для всех 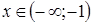, для всех .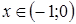

6) Так как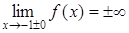

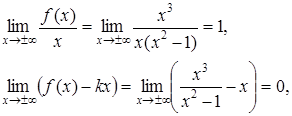
то прямые х = 1 и х = - 1 есть вертикальные асимптоты, график данной функции имеет асимптоту у = х.

7) Найдем производную: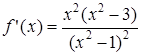

Она существует во всех точках числовой прямой, кроме x = 1 , и равна нулю в точках x = 0, поэтому критическими точками функции будут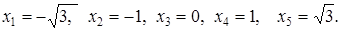

Изучим поведение в окрестности каждой критической точки. Вследствие нечетности достаточно рассмотреть знак на промежутках (- 1; 0), (0; 1), (1; ) , ( ;+∞ ).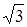

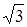Результаты исследования запишем в таблицу:

x	-1< x < 0	х = 0	0< x < 1	1< 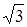x 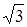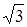<	x =	< x +∞
	-		-	-		+
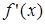
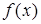
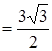
	убывает	Нет экстремума	убывает	убывает	минимум	возростает

В точках х = -1 и х = 1 функция не имеет экстремума, так как эти точки не принадлежат области определения данной функции.

В силу нечетности функции можно утверждать, что при x = - 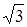эта функция имеет максимум.

8) Чтобы исследовать график функции на выпуклость, найдем вторую производную:

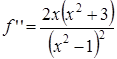
и критические точки данной функции (по второй производной): при 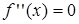х = 0 и 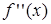не существует при х = ± 1.

Однако точки х = ± 1 не принадлежат области определения функции, поэтому точка перегиба может быть только в точке с абсциссой х = 0.

Исследуем знак второй производной и результаты исследования запишем в таблицу:

x	х < -1	-1 < x < 0	х = 0	0 < x <1	х > 1
	-	+		-	+
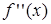
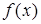
	Выпуклость вверх	Выпуклость вниз	Точка пересечения	Выпуклость вверх	Выпуклость вниз

9) На основе проведенного исследования функции строим ее график (рис. 2).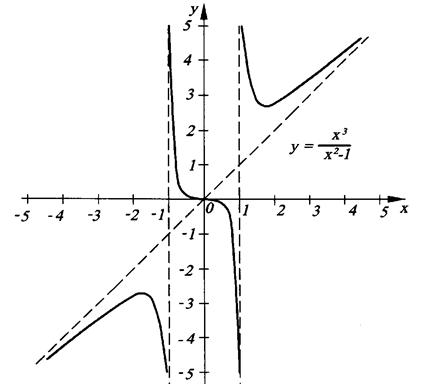

Рисунок 2

Пример 3.

Исследовать функцию 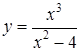и построить ее график.

Решение.

1. Функция определена при любом действительном значении аргумента за исключением 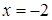и 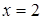. Итак, область определения данной функции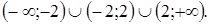

2. Так как , 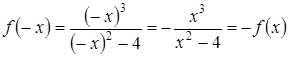то данная функция нечетная и ее график симметричен началу координат. На этом основании можно ограничиться исследованием и построением графика только для 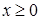. Вторая часть графика (для 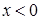) может быть достроена по симметрии.

Функция не периодическая.

3. Найдем точки пересечения 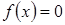с осями координат . Уравнение имеет единое решение, 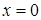, то есть график функции проходит сквозь начало координат 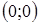. Других точек пересечения графика функции с осями координат нет.

4. Вертикальные асимптоты могут пересекать ось абсцисс в точках . Поскольку предела функции при = 2-0 (слева) и при = 2+0 (справа) бесконечные, то есть. 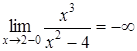и 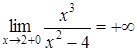, то прямая есть вертикальная асимптота. В силу симметрии графика 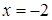также вертикальная асимптота.

5. Поведение функции в бесконечности: .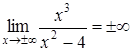

Следовательно, горизонтальных асимптот функция не имеет. Найдем наклонные асимптоты

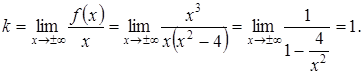
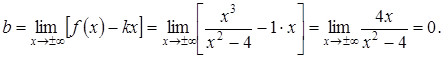
Подставим 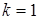и 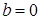в уравнение прямой 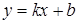. Таким образом, наклонная асимптота графика функции имеет вид .

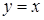6. Интервалы монотонности и экстремумы. Найдем производную функции:

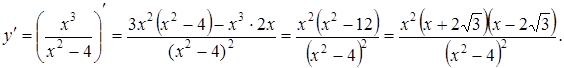
при , та 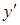- не существует при .

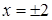Однако критическими являются только точки 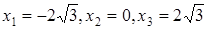(поскольку значения 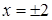не входят в область определения функции).

Исследуем на экстремум только в точку 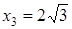(точк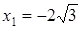и и 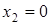на экстремум не исследуем, так как при симметричной достройке графика вопросы о экстремум в этих точках будет решен без использования достаточного условия).

Рассмотрим знаки 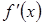в интервалах 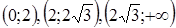и составим таблицу:

x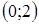
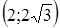
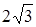
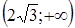
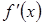
	-	Не существует	-		+
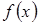
		Не существует		min

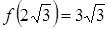
Из таблицы получается, что функция спадает пр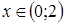и и 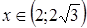, а возрастает при .

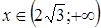Точка - 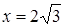точка минимума и 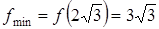минимум функции.

7. Интервалы выпуклости и точки перегиба. Найдем вторую производную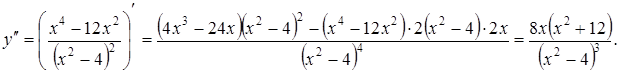

Вторая производная преобразуется в ноль при 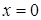и не существует при 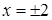, но точки 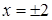не принадлежат области определения.

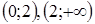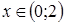Рассмотрим знаки второй производной в интервалах . При график функции на этом интервале выпуклый вверх. При 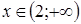график функции на этом интервале выпуклый вниз. Точка - точка перегиба функции в силу симметрии относительно начала координат.

7. Построим график функции для и симметрично отразим его относительно начала координат( рис. 3).

Рисунок 3

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Схема исследования функции.

ОСНОВНЫЕ ТЕРМИНЫ И ПОНЯТИЯ.

область определения функции

четность, нечетность

асимптоты

экстремумы функции

интервалы монотонности функции

интервалы выпуклости функции

ЛИТЕРАТУРА.

1. Кремер М. Ш. "высшая математика для экономистов, Учебник", - М.,: ЮНИТИ, 1998. стр 212-240.

2. Красс М. С. "Математика для экономических специальностей, учебник",-М.: ИНФРА, 1999, стр. 106-110,115-127.

3. В.В. Пак, Ю.Л. Носенко "Высшая математика" Д.: Сталкер, 1997, стр.128-145.

4.А. И.Карасев, З. М. Аксютина, Т. М. Савельева " Курс высшей математики для экономических вузов, ч. 1, м.: ВШ, 1982, стр. 122-145.