
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица 1 - Исходные данные и результаты обработки
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА ДАННЫХ ЭКСПЕРИМЕНТА
Задача: определить параметры вибросита, 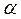 -угол наклона;
-угол наклона; 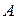 -амплитуду;
-амплитуду;  - частоту, обеспечивающих максимальных объем очищенного раствора
- частоту, обеспечивающих максимальных объем очищенного раствора  .
.
Пределы изменения варьируемых параметров:
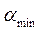 ;
; 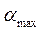
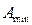 ;
; 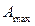
 ;
; 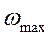
Переход к безразмерным параметрам:
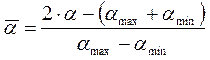
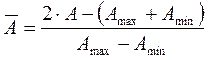
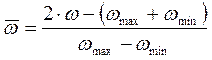


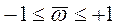
Зависимость 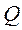 от
от 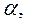
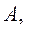
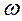 :
: 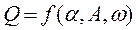 будем искать в виде:
будем искать в виде:
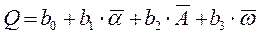 (1)
(1)
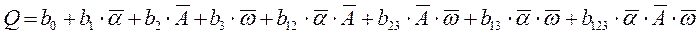 (2)
(2)
Для уравнения (1) необходимо провести 4 опыта
Для уравнения (2) необходимо провести 8 опытов
Опыты будем проводить на нижнем или верхнем значении параметров
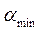 ;
; 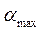
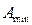 ;
; 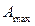
 ;
; 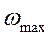
Если опыт проводится на нижнем значении параметра, то его безразмерное значение равно – 1 (-).
Если опыт проводится на верхнем значении параметра, то его безразмерное значение равно + 1 (+).
Матрица планирования экспериментов:
№ опыта, 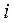
| Параметр 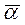
| Параметр 
| Параметр 
| 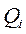
|
| - | - | - | 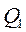
| |
| - | + | - | 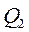
| |
| - | - | + | 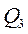
| |
| + | - | - | 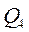
| |
| + | + | - | 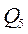
| |
| - | + | + | 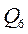
| |
| + | - | + | 
| |
| + | + | + | 
|
В результате проведенного эксперимента имеем систему линейных уравнений:
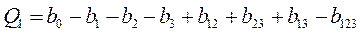 ;
;
 ;
;
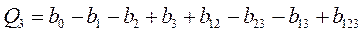 ;
;
 ; (3)
; (3)
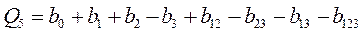 ;
;
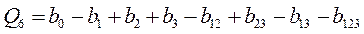 ;
;
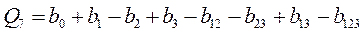 ;
;
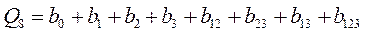 .
.
Решая систему уравнений методом исключения

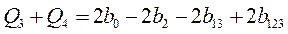
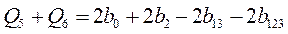
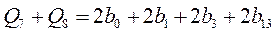
Далее, сложим первое и четвертое уравнения, и сложим второе и третье уравнения:
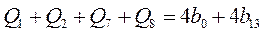
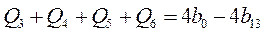
Складывая эти уравнения, найдем:
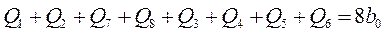 откуда
откуда 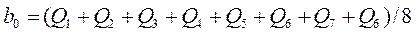
Вычитая эти два уравнения, получим:
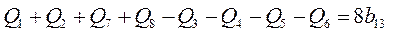 откуда
откуда 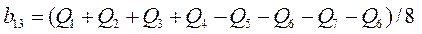
Подставляя найденные значения 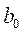 и
и  в систему (3), уже получим не восемь, а шесть уравнений:
в систему (3), уже получим не восемь, а шесть уравнений:
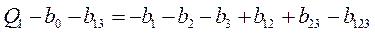 ;
;
 ;
;
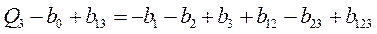 ;
;
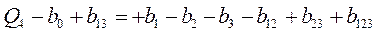 ; (4)
; (4)
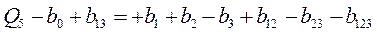 ;
;
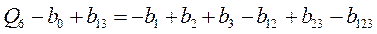 .
.
Аналогично определяются остальные коэффициенты: 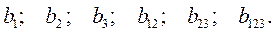
Пусть в результате решения системы уравнений (3) получено (в безразмерных величинах):
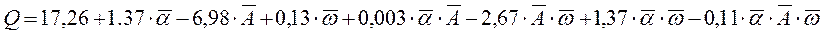 (4)
(4)
Уравнение в размерных величинах получим, если в уравнение (4) подставим зависимости:
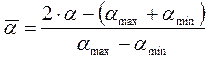

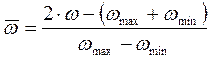
ЛИНЕЙНАЯ РЕГРЕССИЯ
Линейная регрессия(англ.Linear regression)— используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.
Линия регрессии. Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
Y=a+bx.
x называется независимой переменной или предиктором.
Y– зависимая переменная или переменная отклика.
Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y.
- a– свободный член (пересечение) линии оценки; это значение Y, когдаx=0 (Рис.1).
- b– угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Примеры множественной регрессии:
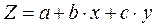 ;
; 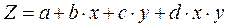
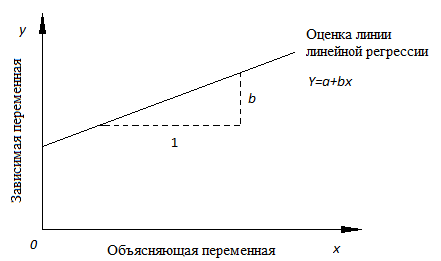
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Регрессионный анализ выполняется на основе выборки ( 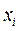 ,
,  ) наблюдений, где a и b– выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
) наблюдений, где a и b– выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
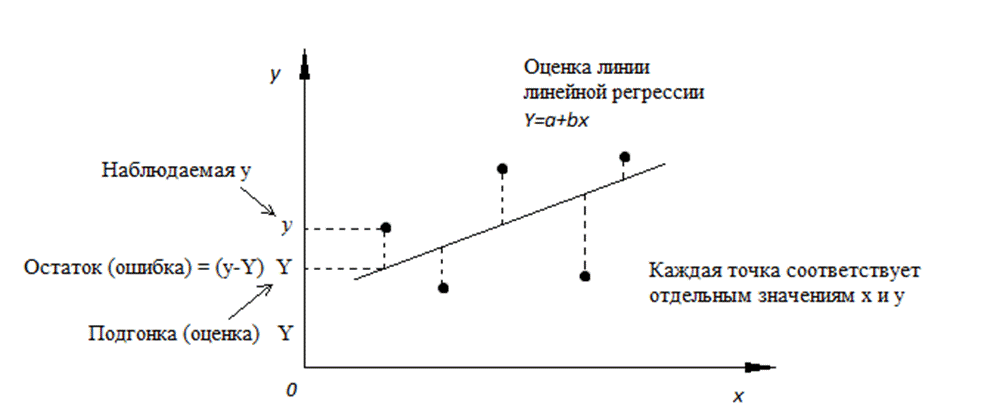
Рис. 2 Линия линейной регрессии с изображенными остатками для каждой точки.
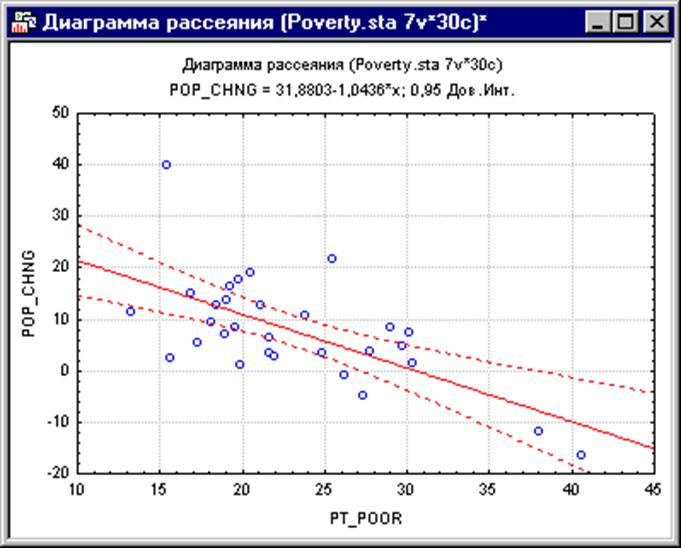
Рис. 3 Результаты обработки
Пусть известна совокупность экспериментальных значений 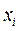 ,
,  ,
, 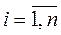
Поиск параметров  и
и 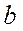 линейной зависимости
линейной зависимости  выполняется путем минимизации функции
выполняется путем минимизации функции
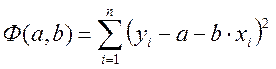 .
.
Дифференцируя функцию 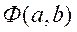 по параметрам
по параметрам  и
и 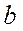 , получаем два линейных относительно
, получаем два линейных относительно  и
и 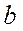 уравнения:
уравнения: 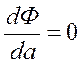
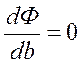
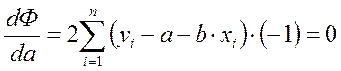 ;
; 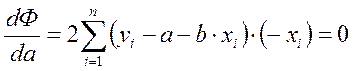
Раскрывая эти уравнения, получим систему двух уравнений:
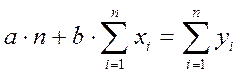 ;
; 
Решая которую, найдем  и
и 
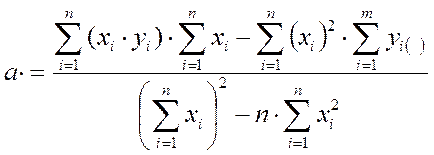 ,
,
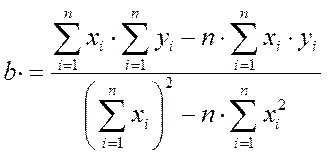
Метод наименьших модулей 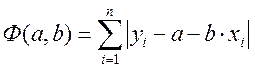
Пример обработки данных методом линейного регрессионного анализа.
Таблица 1 - Исходные данные и результаты обработки
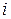
| 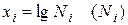
| 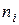
| 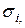 МПа МПа
| 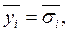 МПа МПа
| 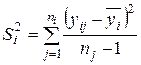
|
| 4,398 (25000) | 173,4; 171,7; 170,7 | 171,9 | 1,865 | ||
| 4,602 (40000) | 152,2; 152,5; 150,0 | 151,6 | 1,865 | ||
| 4,778 (60000) | 129,7; 128,3; 127,2 | 128,4 | 1,570 | ||
| 5,000 (100000) | 108,4; 108,8; 108,9 | 108,4 | 0,07 | ||
| 4,000 (10000) | 212,5; 201,4; 210,7 | 208,2 | 35,44 | ||
| 4,301 (20000) | 173,6; 184,7; 180,9 | 179,7 | 31,85 | ||
| 4,544 (35000) | 147,1; 154,7; 143,9 | 148,6 | 30,77 | ||
| 4,778 (60000) | 123,8; 132,7; 124,5 | 127,0 | 24,49 | ||
| 5,000 (100000) | 112,2; 115,2; 118,2 | 115,2 | 9,0 | ||
S 41,401
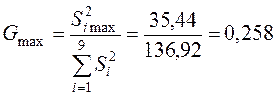 . Обращаясь к статистическим таблице, установим для m=9 и k= n-1=2 критическое значение этого критерия при
. Обращаясь к статистическим таблице, установим для m=9 и k= n-1=2 критическое значение этого критерия при 
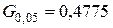 . Поскольку
. Поскольку 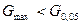 , гипотезу об однородности дисперсий принимаем.
, гипотезу об однородности дисперсий принимаем. .
.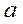 и
и 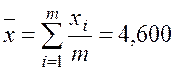 ;
; 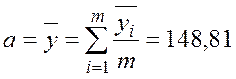 ;
;  ,
, ,
, 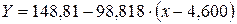
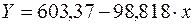 .
.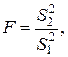 где
где 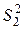 – дисперсия вокруг эмпирической линии регрессии (для ее вычисления заполняются столбцы в таблице 2, начиная с 7-го):
– дисперсия вокруг эмпирической линии регрессии (для ее вычисления заполняются столбцы в таблице 2, начиная с 7-го):
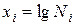
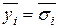
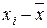

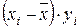
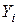
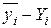

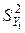
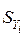

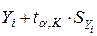
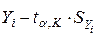
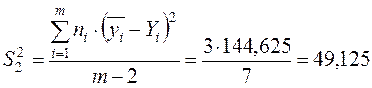 . В результате для F имеем:
. В результате для F имеем: 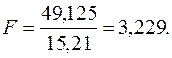
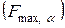 при
при 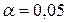 ;
; 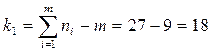 ;
;  определим по статистической таблице:
определим по статистической таблице: 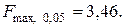
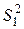 и
и 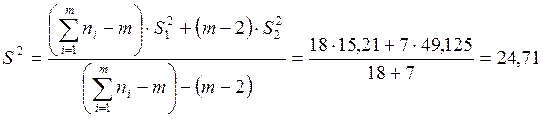 ,
,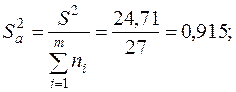
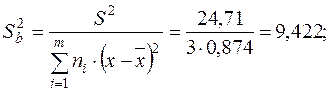
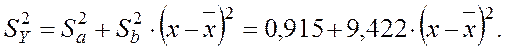
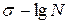 , для этого вычислим значение критерия:
, для этого вычислим значение критерия: 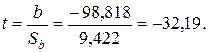
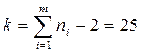 и уровня значимости
и уровня значимости 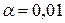 получим табличное значение критерия Стьюдента:
получим табличное значение критерия Стьюдента:  . Поскольку
. Поскольку 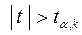 , то коэффициент b значим.
, то коэффициент b значим.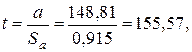
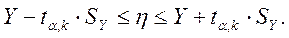
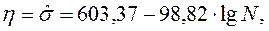 (1)
(1)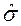 – оценка действующего напряжения (МПа), N – число циклов нагружения. Учитывая полученную выше зависимость для оценки дисперсии
– оценка действующего напряжения (МПа), N – число циклов нагружения. Учитывая полученную выше зависимость для оценки дисперсии 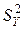 , для расчета границ доверительных интервалов получим следующие уравнения (индекс "-" соответствует нижней, а "+" -верхней границе):
, для расчета границ доверительных интервалов получим следующие уравнения (индекс "-" соответствует нижней, а "+" -верхней границе):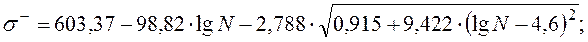 (2)
(2)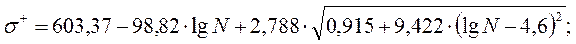
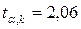 :
: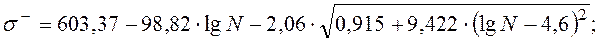 (3)
(3)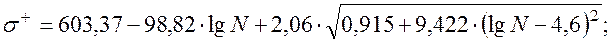
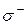 ,
, 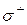 , определенные по приведенным формулам, поместим в 13 и 14 столбцы таблицы 2 (верхнее значение в каждой i-й строке соответствует 99% вероятности, а нижнее – 95%).
, определенные по приведенным формулам, поместим в 13 и 14 столбцы таблицы 2 (верхнее значение в каждой i-й строке соответствует 99% вероятности, а нижнее – 95%).