СТАТИЧЕСКИЕ ОПРЕДЕЛИМЫЕ ПЛОСКИЕ

СТАТИЧЕСКИЕ ОПРЕДЕЛИМЫЕ ПЛОСКИЕ

БАЛОЧНЫЕ ФЕРМЫ

Фермой называется стержневая система, которая остается геометрически неизменяемой после условной замены в расчетной схеме жестких узлов идеальными шарнирами.

Преимущества ферм по сравнению с балками очевидны:

- При узловом приложении нагрузки – стержни фермы работают на растяжение - сжатие.

- Напряжения распределяются равномерно.

- Уменьшается собственный вес конструкции.

- Увеличивается жесткость конструкции.

- Легкость, экономичность, возможность высокой заводской готовности.

Цель расчета фермы - определение усилий во всех стержнях фермы.

Расчет выполняется аналитически, геометрически (построением диаграммы Максвелла-Кремоны), с помощью линий влияния, кинематически…

Аналитический расчет фермы обобщил в 1850-х г.г. Д.И.Журавский.

В основу расчета ферм положены следующие упрощения:

- стержни в узлах фермы соединены идеальными шарнирами;

- фермы рассчитываются только на узловое приложение нагрузки,

- стержни фермы работают только на растяжение сжатие, т.е. в

стержнях ферм возникают только продольные силы N;

- Расчет начинают с определения опорных реакций. Опорные реакции в ферме определяются так же, как в балке. Для определения опорных реакций составляют уравнения статического равновесия: сумма моментов всех сил, приложенных к ферме относительно опорных точек и сумма проекций всех сил на ось должны быть равны нулю

Определение усилий в стержнях фермы возможно только после определения опорных реакций. Опорные реакции определяются в балочной ферме так же, как в простой балке:

для этого составляем уравнения статического равновесия, аа именно: рассматриваем сумму моментов всех сил, приложенных к ферме, относительно опорных точек А и В, а также сумму проекций всех сил на горизонтальную ось:

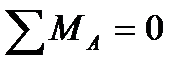
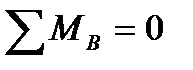
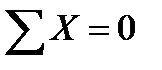
для проверки найденных опорных реакций составляем еще одно уравнение статического равновесия, а именно – сумма проекций всех сил, приложенных к ферме, на вертикальную ось должна равняться нулю:

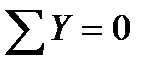
Аналитическое определение усилий в стержнях простых ферм производится одним из двух основных методов: методом круговых сечений (его еще называют методом вырезания узлов) или методом сквозных сечений (его еще называют методом сечений)

1) Метод вырезания узлов (метод круговых сечений) – заключается в том, что производится вырезание узла, в котором сходятся не более двух неизвестных усилий. При этом в рассеченных стержнях «открываются» усилия – они обозначаются стрелками, направленными от узла вдоль оси соответствующего стержня – такое направление усилия принято считать положительным. Затем составляются уравнения статического равновесия: сумма проекций всех сил, приложенных к узлу на любую ось должна равняться нулю:

å X =0

å Y =0

2) Метод сквозных сечений (для краткости этот метод называют «метод сечений»)– заключается в том, что проводиться сквозное сечение таким образом, чтобы рассеченными оказались не более трех стержней., не пересекающихся в одной точке. При этом в рассеченных стержнях «открываются» усилия – они обозначаются стрелками, направленными от узла вдоль оси соответствующего стержня – такое направление усилия принято считать положительным. При этом возможны два основных способа определения усилий: способ моментной точки и способ проекций.

а) Если оси двух из трех рассеченных стержней, за исключением, того, усилие в котором определяется, пересекаются в одной точке К, то точка К называется моментной ( в курсе теоретической механики ту же точку принято называть точкой Риттера). Относительно этой точки составляются уравнения статического равновесия: сумма моментов всех сил, приложенных по одну строну от сечения, должна быть равна нулю:

∑М_{к лев}=0

∑М_{к пр}=0

Такой способ определения усилий в стержнях фермы называется «способ моментной точки». Способ моментной точки является приоритетным, но в некоторых случаях положение моментной точки определить невозможно, в частности, если два других стержня параллельны.

В этом случае используется способ проекций:

б) Способ проекций применяется для расчета в том случае, если два из трех рассеченных стержней, за исключением искомого, не пересекаются в одной точке, например в ферме с параллельными поясами. При этом составляют уравнения статического равновесия: сумма проекций всех сил, приложенных по одну сторону от сечения на любую ось должна быть равна нулю:

å X =0

å Y =0

При расчете ферм предпочтение отдается методу сечений и способу моментной точки. Если оси двух стержней не пересекаются, используется способ проекций.

И только в том случае, если воспользоваться методом сечений невозможно, расчет проводят методом вырезания узлов.

Теперь переходим к определению усилий в стержнях фермы – порядок действий можно представить в следующей схеме:

12 Следующая ⇒