Основные задачи

Основные задачи

Обычно решение задач по теме «методы изображений» разделяют на два этапа: анализ и построение. Анализ или поиск решения задачи состоит в установлении таких свойств оригинала, которые, сохраняясь на изображении, однозначно его определяют. Построение состоит в последовательном перечислении всех этапов решения задачи. При этом выполняется чертеж. таким образом, шаг за шагом осуществляется построение изображения данной фигуры с помощью циркуля и линейки.

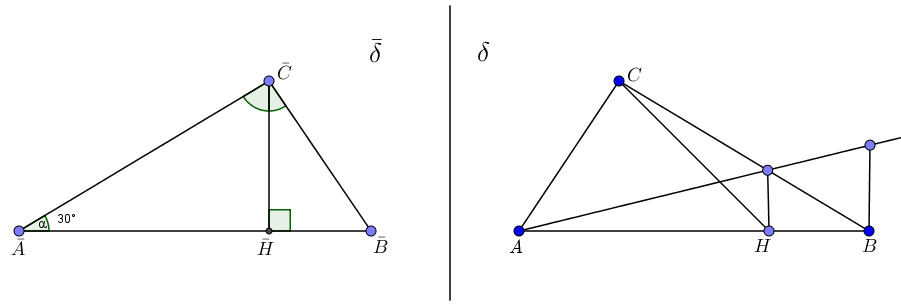
Задача 1. Дано изображение прямоугольного треугольника с острым углом 30⁰. Построить изображение высоты, проведенной из вершины прямого угла.

Решение.Анализ. Пусть треугольник 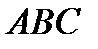является изображение треугольника 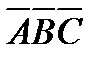с прямым углом 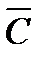и углом 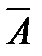равным 30⁰. Проведем высоту 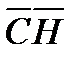оригинала. Известно, что в прямоугольном треугольнике катет, лежащий против угла в 30⁰ равен половине гипотенузы.

Применяя это свойство последовательно к треугольникам 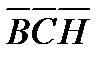и 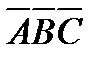находим: 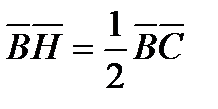и 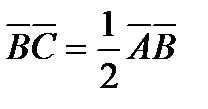. Отсюда 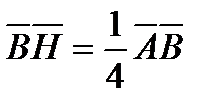(рис. 74).

Построение. На отрезке 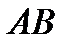строим точку 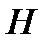, удовлетворяющую условию 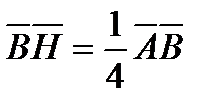. Тогда отрезок 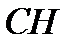– искомое изображение высоты (рис. 75).

Рис. 74. Рис. 75.

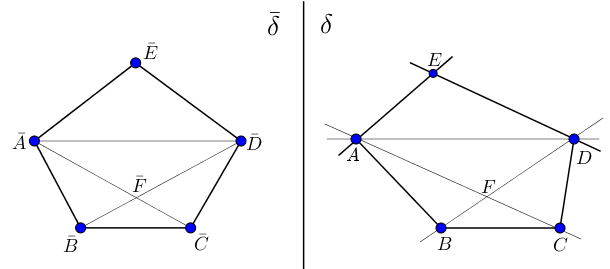
Задача 2. Построить изображение правильного пятиугольника.

Решение.Анализ. Пусть 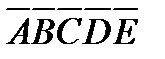есть правильный пятиугольник-оригинал со стороной 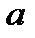. Все его диагонали имеют равную длину, которую обозначим 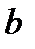. Рассмотрим точку 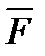пересечения диагонале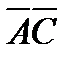й и 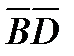. Путем непосредственного подсчета величин углов легко доказать, что если диагональ и сторона правильного пятиугольника не имеют общей вершины, то они лежат на параллельных прямых. В частности, четырехугольник 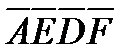является ромбом со стороной 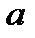. Далее треугольник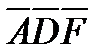и и 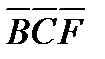подобны, следовательно, 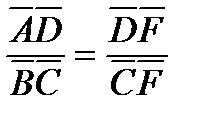или 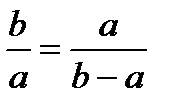. Получим уравнение 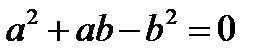, из которого находим 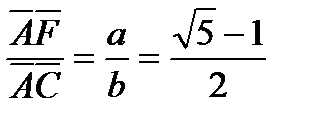(рис. 76).

Построение. Строим:

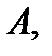
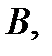
1) Произвольно три точки 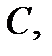не лежащие на одной прямой.

2) Точку 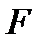на отрезке 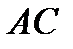так, чтобы .

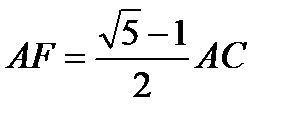3) Точку 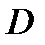на пересечении прямой 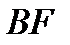и прямой, проходящей через точку 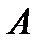параллельно прямой .

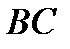4) Точку 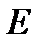пересечения двух прямых, первая из которых проходит через точку 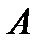параллельно прямой 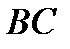, а вторая – через точку 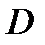параллельно прямой .+

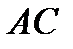Тогда 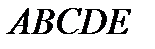изображение данного пятиугольника (рис. 77).

Рис. 76. Рис. 77.

Задача 5. Построить изображение правильного треугольника, вписанного в окружность.

Решение.Анализ. Пусть треугольник 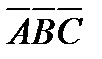есть правильный треугольник-оригинал, вписанный в окружность 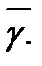Отметим, что центр 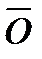этой окружности является точкой пересечения медиан и высот треугольника 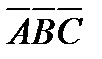. Есл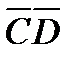и и 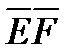перпендикулярные диаметры окружности 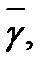то прямые 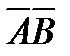и 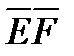параллельны. Далее, обозначим 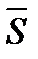середину отрезк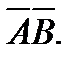а Тогда 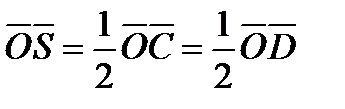(рис. 82).

Построение. Строим:

1) Произвольный эллипс 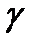и его центр O.

2) Произвольную точку 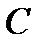эллипса .

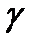3) Сопряженные диаметры 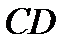и 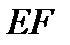эллипса .

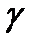4) Середину 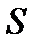отрезка .

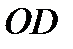5) Точк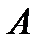и и 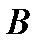пересечения эллипса 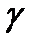ходящей через точку 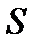параллельно прямой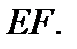

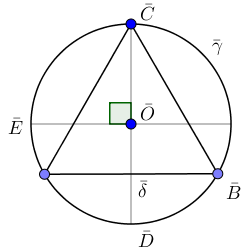
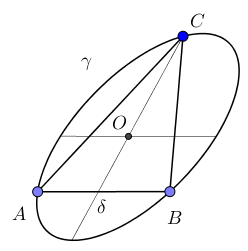
Тогда ABC изображение данного треугольника (рис.83).

Рис. 82. Рис. 83.