
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица 2
ЗАДАЧА 1. Определить критерии подобия (безразмерные комбинации) по следующим данным. [1, стр. 27-29].
1. Потери напора Н при движении жидкости по каналу являются Функцией длины l, гидравлического радиуса R сечения канала, скорости жидкости U и коэффициента Шези С: Н = f(l, R, U, С).
Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид: [H] = L; [l] = L; [R] = L; [U] =LT-1; [C] = L0.5T-1.
2. Потери давления р при движении жидкости по трубопроводу круглого сечения являются функцией плотности жидкости  , длины l и диаметра d трубопровода, средней скорости жидкости U; р = f(
, длины l и диаметра d трубопровода, средней скорости жидкости U; р = f(  ,l,d,U). Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
,l,d,U). Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
[p] = МL-1T-2; [  ] = МL-3; [l] = L; [d] = L; [U] = LT-1.
] = МL-3; [l] = L; [d] = L; [U] = LT-1.
3. Повышение давления 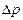 в трубе при прямом гидравлическом ударе (tз дк <t = 2l/c) является функцией плотности жидкости
в трубе при прямом гидравлическом ударе (tз дк <t = 2l/c) является функцией плотности жидкости  , модуля упругости жидкости Е0, внутреннего диаметра d и толщины стенки
, модуля упругости жидкости Е0, внутреннего диаметра d и толщины стенки 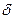 трубы, модуля упругости материала стенок трубы E, значения погашенной скорости U:
трубы, модуля упругости материала стенок трубы E, значения погашенной скорости U: 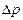 = f(
= f(  , Е0, d,
, Е0, d, 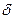 , E, U). Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
, E, U). Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
[ 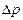 ] = МL-1T-2; [
] = МL-1T-2; [  ] = МL-3; [Е0] = МL-1T-2; [d] = L; [
] = МL-3; [Е0] = МL-1T-2; [d] = L; [ 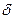 ] = L; [Е] = МL-1T-2; [U] = LT-1.
] = L; [Е] = МL-1T-2; [U] = LT-1.
4. Скорость распространения ударной волны C возникающей в жидкости при гидравлическом ударе, зависит от рода жидкости /плотности  /, материала, диаметра и толщины стенок трубы /модуля упругости материала стенок трубы E диаметра d и толщины
/, материала, диаметра и толщины стенок трубы /модуля упругости материала стенок трубы E диаметра d и толщины 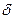 стенок трубы/, модуля упругости жидкости Е0:
стенок трубы/, модуля упругости жидкости Е0:
С = f(  , E, d,
, E, d, 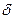 , Е0)
, Е0)
Найти безразмерные коэффициенты, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
[С] = LT-1; [  ] = МL-3; [Е] = МL-1T-2; [d] = L; [
] = МL-3; [Е] = МL-1T-2; [d] = L; [ 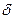 ] = L; [Е0] = МL-1T-2.
] = L; [Е0] = МL-1T-2.
5. Сила сопротивления R при движении вязкой жидкости является функцией скорости жидкости U, живого сечения 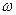 , плотности
, плотности  и динамической вязкости
и динамической вязкости 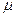 жидкости, ускорения свободного падения g, давления р:
жидкости, ускорения свободного падения g, давления р:
R = f(U, 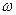 ,
,  , g,
, g, 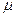 , р)
, р)
Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
[R] = MLT-2; [U] = LT-1; [ 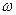 ] = L2; [
] = L2; [  ] = МL-3; [g] = LT-2; [
] = МL-3; [g] = LT-2; [ 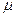 ] = МL-1T-1; [p] = МL-1T-2.
] = МL-1T-1; [p] = МL-1T-2.
6. Расход воды Q через цилиндрический насадок является функцией диаметра dн насадка, плотности  к динамической вязкости
к динамической вязкости 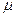 и жидкости, давления p перед насадком:
и жидкости, давления p перед насадком:
Q = f(dн,  ,
, 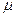 , p)
, p)
Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
[Q] = L3T-1; [dн] = L; [ 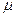 ] = МL-1T-1; [
] = МL-1T-1; [  ] = МL-3; [p] = МL-1T-2.
] = МL-3; [p] = МL-1T-2.
7. Среднее значение ЭДС самоиндукции eL для машин постоянного тока является функцией окружной скорости якоря Ua, длины якоря l, линейной нагрузки якоря A и магнитной проводимости 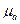 :
:
eL= f(Ua, l, A, 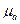 ) при заданном числе витков в секции
) при заданном числе витков в секции 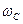 .
.
Найти безразмерные комбинации, описывающие процесс, если размерности фундаментальных физических переменных имеют вид:
[eL] = L2МT-3I-1; [Ua] = LT-1; [l] = L; [A] = L-1I; [ 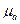 ] = LМT-2I-2.
] = LМT-2I-2.
8. Известно, что усилие избыточного давления, действующее со стороны жидкости на плоскую стенку, зависит от высоты h слоя над центром тяжести смоченной поверхности, площади S этой поверхности, плотности жидкости  и ускорения свободного падения g:
и ускорения свободного падения g: 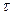 = f(h, S,
= f(h, S,  , g). Найти безразмерные комбинации, которым описывается процесс, если размерности фундаментальных физических переменных имеют вид:
, g). Найти безразмерные комбинации, которым описывается процесс, если размерности фундаментальных физических переменных имеют вид:
[ 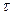 ] = МLT-2; [h] = L; [S] = L2; [
] = МLT-2; [h] = L; [S] = L2; [  ] = МL-3; [g] = LT-2.
] = МL-3; [g] = LT-2.
9. Расход воды Q через прямоугольный водослив является функцией плотности  , вязкости
, вязкости 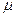 жидкости, высоты h воды над порогом, ширины b порога и ускорения свободного падения g: Q = f(
жидкости, высоты h воды над порогом, ширины b порога и ускорения свободного падения g: Q = f(  ,
, 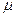 , h, b, g). Найти безразмерные комбинации, которыми описывают процесс, если формулы размерностей физических величин имеют вид:
, h, b, g). Найти безразмерные комбинации, которыми описывают процесс, если формулы размерностей физических величин имеют вид:
[Q] = L3T-1; [  ] = МL-3; [
] = МL-3; [ 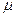 ] = МL-1T-1; [h] = L; [g] = LT-2.
] = МL-1T-1; [h] = L; [g] = LT-2.
10. Пластина площадью S движется относительно неподвижной смоченной жидкостью плоской поверхности со скоростью U. Толщина слоя h вязкость 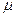 . Усилие, приложенное к пластине определяется функцией вида F = f(S, U, h,
. Усилие, приложенное к пластине определяется функцией вида F = f(S, U, h, 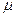 ). Найти безразмерные комбинации, которыми описывают процесс, если формулы размерностей физических переменных имеют вид:
). Найти безразмерные комбинации, которыми описывают процесс, если формулы размерностей физических переменных имеют вид:
[F] = МLT-2; [S] = L2; [U] = LT-1; [h] = L; [ 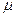 ] = МL-1T-1.
] = МL-1T-1.
11. К веревке длиной R, один конец которой прикреплен к неподвижной точке, привязан камень массой m. Камень вращается со скоростью U. Ускорение свободного падения равно g, а сила натяжения веревка, определяемая в опыте, F = f(R, m, U, g). Найти безразмерные комбинации, которыми можно описать процесс. Формулы размерностей физических переменных.
[F] = МLT-2; [R] = L; [m] = M; [U] = LT-1; [g] = LT-2.
12. Расход воды Q через цилиндрический насадок зависит от его диаметра d, диаметра трубопровода D , напора перед насадком H и ускорения свободного падения g: Q = f(d, D, H, g). Найти безразмерные комбинации, которыми можно описать процесс, Формулы размерностей физических переменных:
[Q] = L3T-1; [d] = L; [D] = L; [H] = L; [g] = LT-2.
13. Мощность на валу насоса N зависит от создаваемого им напора H, подачи Q, плотности жидкости  и ускорения свободного падения g: N = f(H, Q,
и ускорения свободного падения g: N = f(H, Q,  , g). Найти безразмерные комбинации, которыми описывается процесс, если формулы размерностей физических переменных имеют вид:
, g). Найти безразмерные комбинации, которыми описывается процесс, если формулы размерностей физических переменных имеют вид:
[N] =ML2T-3; [H] = L; [Q] = L3T-1; [  ] = МL-3; [g] = LT-2.
] = МL-3; [g] = LT-2.
14. Время t продолжительности опорожнения вертикального цилиндрического бака зависит от диаметра D бака, уровня H жидкости, диаметра отверстия d в дне бака, ускорения свободного падения g: t = f(D, H, d, g)
Найти безразмерные комбинации, которыми описывается процесс, если формулы размерностей физических переменных имеют вид:
[t] = T; [D] = L; [H] = L; [d] = L; [g] = LT-2.
15. Сила сопротивления трения Fтр тонкой прямоугольной пластины, обтекаемой потоком жидкости, зависит от площади боковых поверхностей пластины 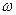 , плотности
, плотности  и скорости U жидкости, ускорения свободного падения g:
и скорости U жидкости, ускорения свободного падения g:
Fтр = f( 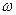 ,
,  , U, g)
, U, g)
Найти безразмерные комбинации, которыми описывается процесс. Формулы размерностей физических переменных:
[Fтр] =MLT-2; [ 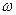 ] = L2; [
] = L2; [  ] = МL-3; [g] = LT-2; [U] = LT-1.
] = МL-3; [g] = LT-2; [U] = LT-1.
ЗАДАЧА 2.Определить математическое ожидание, дисперсию, построить полигон, гистограмму, график нормального закона распределения по экспериментальным данным. Число измерений составляет сто. [1, стр. 41-45].
ПРИМЕР.
Методика решения
1. Экспериментальные данные рекомендуется сгенерировать с пакете MS Exel. Для этого используется меню «Анализ данных», в нем необходимо сгенерировать массив, указать количество точек - 100, вид распределения – нормальное и т.д. «Анализ данных» устанавливается через главное меню Exel – настройки – надстройки – Анализ данных – Генерация случайных чисел.
2. Весь диапазон значений величин делят на равные интервалы. Число интервалов рекомендуется принимать
К = 1 + 3, 32lg n,
где n - число измерений. Принимаем целое число интервалов.
3. Затем для каждого интервала определяют количество приходящихся измерений nU. Отношение этой величины к общему числу измерений n равно вероятности попадания единичных измерений в соответствующий интервал. Относительную частоту попадания или оценку вероятности попадания единичных измерений в соответствующий интервал можно получить, разделив Pu* на величину интервала (52,2-49,0/К=0,4).
Результаты измерений и вероятностей заносим в таблицу.
Таблица (ПРИМЕР)
| Показатель
| Диаметр стержня, мм | |||||||
| 49,0 49,4 | 49,4 49,8 | 49,8 50,2 | 50,2 50,6 | 50,6 51,0 | 51,0 51,4 | 51,4 51,8 | 51,8 52,2 | |
| Число измерений в интервале nU | ||||||||
| Вероятность попадания в интервал, Pu* | 0,071 | 0,125 | 0,196 | 0,286 | 0,178 | 0,108 | 0,036 | 0,018 |
| Оценка вероятности, рu* | 0,178 | 0,313 | 0,49 | 0,715 | 0,445 | 0,27 | 0,09 | 0,045 |
4. По полученным результатам строят: полигон (рис. 1, а), гистограмму (рис. 1, б) и график нормального закона распределения (закон Гаусса). Для построения закона Гаусса необходимо вычислить параметры нормального закона: mx и σ (математическое ожидание и среднеквадратическое отклонение) для ста измерений.

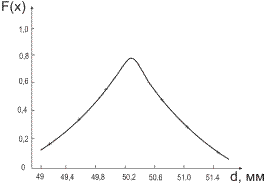
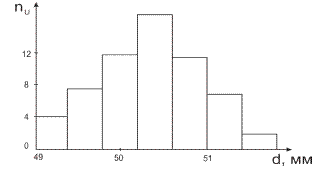
Рисунок 1 - Закон распределения вероятностей дискретной случайной величины, представленный в форме полигона (а) и гистограммы (б)
ЗАДАЧА 3. В одинаковых условиях проведены испытания двух объектов. Получены равновероятностные данные об их производительности (табл.1). Сравнить результаты испытаний и дать заключение об их статистическом различии. [1, стр. 61-63].
Таблица 1
| Номер варианта | Производительность, т/ч | |||||
| Номер опыта | ||||||
| 57* | ||||||
* Примечание. Верхнее число в опытах приведено для объекта № 1, нижнее - для объекта № 2.
Задача 4.В результате испытаний центробежного насоса установлено с равной вероятностью, что создаваемый им напор при соответствующих подачах определяется значениями, приведенными в табл.2. Известно также, что напор насоса при его испытаниях измерялся прибором, класс точности и предел измерения которого указаны в таблице.
Установить аналитическую зависимость напора Н от подачи Q. [1, стр. 73-76].
Таблица 2
| Вариант | Напор насоса Н, м. вод. ст., при подаче Q, м3/ч | Класс точности и предел измерения прибора, м. вод. ст. | ||||
| 3.0 100.0 | ||||||
| 2.0 150.0 | ||||||
| 2.0 160.0 | ||||||
| 2.5 100.0 | ||||||
| 3.0 100.0 | ||||||
| 2.5 140.0 | ||||||
| 3.0 125.0 | ||||||
| 2.0 150.0 | ||||||
| 2.5 150.0 | ||||||
| 2.5 125.0 | ||||||
| 2.0 160.0 | ||||||
| 1.5 200.0 | ||||||
| 2.0 200.0 | ||||||
| 2.5 200.0 | ||||||
| 2.0 250.0 | ||||||
| 2.0 200.0 | ||||||
| 1.5 300.0 | ||||||
| 2.5 250.0 | ||||||
| 2.0 280.0 | ||||||
| 2.5 250.0 | ||||||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|