
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 9 – решение. Задание 9 № 10244. Решение.. Приведем другое решение.. Задание 9 № 10245
Задание 9 – решение
Задание 9 № 10244
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город В?
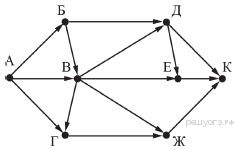
Решение.
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом если путь должен не проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
А = 1
Б = А = 1
В = А + Б = 2
Г = В = 2 (А не учитываем, поскольку путь должен проходить через город В)
Д = В = 2 (Б не учитываем, поскольку путь должен проходить через город В)
Е = В + Д = 4
Ж = В + Г = 4
К = Д + Е + Ж = 2 + 4 + 4 = 10.
Приведем другое решение.
Количество путей из города А в город К, проходящих через город В, равно произведению количества путей из города А в город В и количества путей из города В в город К.
Найдем количество путей из города А в город В:
А = 1
Б = А = 1
В = А + Б = 2
Найдем количество путей из города В в город К (при этом В - исходный пункт):
В = 1
Г = В = 1
Ж = В + Г =1 + 1 = 2
Д = В = 1
Е = В + Д = 1 + 1 = 2
К = Д + Е + Ж = 1 + 2 + 2 = 5
Тогда количество путей из города А в город К, проходящих через город В, равно 2 · 5 = 10.
Ответ: 10.
Задание 9 № 10245
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З и И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И, проходящих через город В?
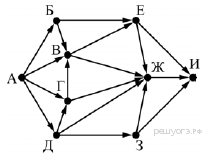
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|