Непрерывные случайные величины

§2. Непрерывные случайные величины

Множество значений непрерывной случайной величины непрерывно. Этолибо отрезок, либо луч, либо вся числовая прямая R

Непрерывная случайная величина может быть задана с помощью плотности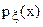

Условие нормировки: (2.1)

(если плотность задана с точностью до константы, то константа ищется из условия нормировки)

Пример: Непрерывная случайная величина задана своей плотностью

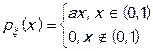
Постоянная а неизвестна

Ищем её из условия нормировки

Подставляем нашу плотность

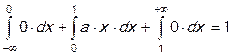
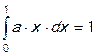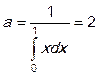
Для непрерывной случайной величины также можно вычислить основные числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение)

- формула для расчёта математического ожидания непрерывной случайной величины (2.2)

В нашем примере:

-среднее ожидаемое значение

формула для расчёта дисперсии непрерывной случайной величины это расчётная формула . можно считать и по формуле

но по расчётной проще т.к. матожидание у нас уже подсчитано

В нашем примере:

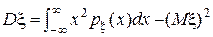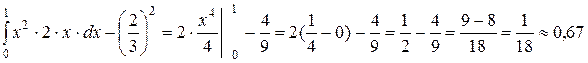
- средний разброс случайной величины своего относительно математического ожидания в квадрате

Среднее квадратическое отклонение – это корень из дисперсии (это средний разброс с.в. относительно своего математического ожидания). В нашем примере

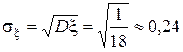
Расчет вероятности попасть в интервал производится по формуле:

(2.4)

В нашем примере:

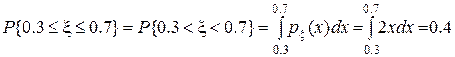вероятность в непрерывном случае не зависит принадлежат концы интервалу или нет