
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Группа 1БУ-67. Тема: Показательные уравнения.. Показательные уравнения
Группа 1БУ-67
Тема: Показательные уравнения.
Задание:
1. Изучить теоретические сведения.
2. Записать примеры выполнения заданий.
3. Выполнить задания.
4. Выполненные задания сфотографировать и отправлять на электронную почту tryufelka83@mail.ru или в ЛС социальной сети VKontakte.
5. Выполненные задания сдать до: 22.10
Учебник: Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014.
Ссылка на учебник онлайн:
https://uchebnik-skachatj-besplatno.com/Алгебра/Учебник%20Алгебра%2010-11%20класс%20Алимов%20Колягин/index.html#prettyPhoto
С. 77-78
Вспомните свойства степеней с действительным показателем.
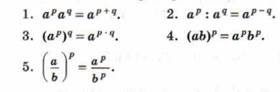
Показательные уравнения
Уравнение, которое содержит переменную в показателе степени, называется показательным уравнением.
Простейшее показательное уравнение имеет вид ax = b,где a > 0, a ≠ 1.
Пример: 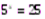 .
. 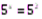 ;
; 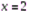 . Ответ:
. Ответ: 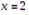 .
.
Пример: 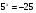 , т.к. -25<0, то уравнение не имеет корней.
, т.к. -25<0, то уравнение не имеет корней.
Ответ: корней нет.
Методы решения показательных уравнений:
1. Метод приведения к одному основанию;
2. Метод вынесения за скобки;
3. Метод приведения к квадратному уравнению.
Рассмотрим 1 метод. Метод приведения к одному основанию.
При a > 0, a ≠ 1, уравнения a f(x) = a g(x) и f(x) = g(x) равносильны.
Пример. Простейшие уравнения: (устно)
а)2х-5 = 16 Приведение обеих частей к общему основанию: 2х-5 = 24
Данное уравнение равносильно уравнению: х-5 = 4, х = 9.Ответ: 9.
б)3х = -9
Так как показательная функция принимает только положительные значения, то данное уравнение не имеет решений. Ответ: нет решений.
Пример.
1) 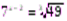 .
. 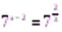 ;
; 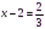 ;
; 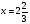 . Ответ:
. Ответ: 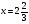 .
.
2) 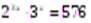 .
. 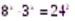 ;
; 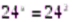 ; x=2. Ответ: x=2.
; x=2. Ответ: x=2.
3) 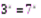 .
. 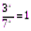 ;
; 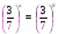 ; x=0. Ответ: x=0.
; x=0. Ответ: x=0.
4) 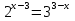
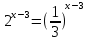
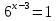
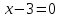
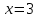
Рассмотрим 2 метод. Метод вынесения за скобки.
Пример. Решить уравнения a) 2x+1 - 2x + 2x-2 - 2x-3 = 9,
Решение. a) Перепишем уравнение в виде 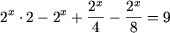
или 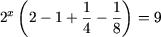 откуда
откуда 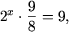 следовательно 2x = 8 или x = 3.
следовательно 2x = 8 или x = 3.
Рассмотрим 3 метод. Метод приведения к квадратному уравнению.
Пример. Уравнения, решаемые с помощью введения новой переменной.
16х – 17 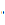 4х + 16 = 0
4х + 16 = 0
Пусть 4х = t, где t 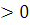 , тогда уравнение примет вид: t2 - 17t + 16 = 0
, тогда уравнение примет вид: t2 - 17t + 16 = 0
Данное квадратное уравнение является приведенным, по теореме Виета получим:
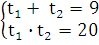
t1=1, t2=16
Если t1 = 1, то 4х = 1, 4х = 40, х1 = 0. Если t1 = 16, то 4х = 16, 4х = 42, х2 = 2 Ответ: х1 = 0, х2 = 2.
Пример.Решить уравнение 64·9x -84·12x +27·16x = 0,
Решение. Записав уравнение в виде
64·32x -84·3x ·4x +27·42x = 0
и разделив на 42x, получим
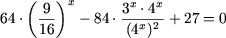
или
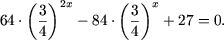
Обозначив 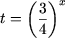 получим квадратное уравнение
получим квадратное уравнение
64t2-84t+27 = 0.
Дискриминант данного уравнения равен D = 842 -4·64·27 = 42· 32·72 -4·4·16·9·3 = 42·32(49-48) = 122, а значит его корни имеют вид
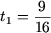 и
и 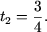
Таким образом
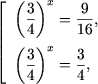
откуда x1 = 2 и x2 = 1.
Домашнее задание.
Решить уравнения
1) 0,35-2х = 0,09;
2) 225 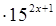 = 1;
= 1;
3) 3х-2 – 3х-3 = 6;
4) 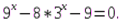
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|