Дифференциал функции

Дифференциал функции

1. Определение и геометрический смысл

ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке может быть записано как сумма линейной относительно Δx части и бесконечно малой более высокого порядка чем Δx , т.е.

Δf(x₀) = A ⋅ Δx + β(Δx) , (1)

где A – число, β(Δx) – б.м. более высокого порядка чем Δx.

Слагаемое A ⋅ Δx в выражении (1) (т.е. линейную относительно Δx часть Δf(x₀)) называют дифференциалом функции y = f(x) вточке x₀иобозначают: dy(x₀) , df(x₀) .

ТЕОРЕМА 1 (о связи дифференцируемости с существованием производной).

Функция y = f(x) дифференцируема в точке x₀⇔ она имеет в точке x₀производную. При этом для ее дифференциала в точке x₀справедливо равенство

dy(x₀) = f ′(x₀) ⋅ Δx . (2)

ДОКАЗАТЕЛЬСТВО

Очевидно, что соответствие (x₀; Δx) → df(x₀) является функцией (двух переменных).

Ее называют дифференциалом функции y = f(x) и обозначают

dy , df(x) .

Замечание. Из теоремы 1 следует, что нахождение производной и дифференциала функции представляет собой по существу одну и ту же задачу. Поэтому операцию нахождения производной называют дифференцированием функции.

ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется дифференцируемой на интервале (a;b)если она дифференцируема (т.е. имеет производную) в каждой точке этого интервала.

Функция y = f(x) называется дифференцируемой на отрезке [a;b]если она дифференцируема на интервале (a;b) и имеет соответствующие односторонние производные в точках a и b.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА

Рассмотрим график функции y = f(x).

Пусть функция y = f(x) дифференцируема в точке x₀.

Тогда в x₀функция f(x) имеет производную f ′(x₀) .

⇒ в точке M₀(x₀; f(x₀)) ∃ касательная к кривой y = f(x).

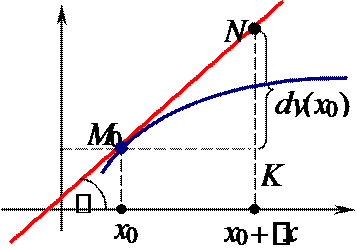
Таким образом, дифференциал функции y = f(x) в точке x₀равен приращению ординаты точки на касательной к кривой y = f(x), которое соответствует приращению Δx.

Замечания.

1) Так как для дифференциала функции y = x справедливо dy = dx = Δx ,

то говорят: «дифференциал независимой переменной равен ее приращению».

Учитывая этот факт, формулу (2) можно переписатьввиде

dy = f ′(x) ⋅ dx . (3)

2) Из формулы (3) получаем, что производная y ′ = f′(x) является отношением 2-хдифференциалов:

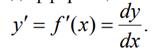
Таким образом, символическая дробь превратилась в реальнуюдробь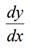

2. Свойства дифференциалов

1) Дифференциал константы равна нулю, т.е. d(C) = 0 , где C – константа.

2) Дифференциал суммы (разности) равна сумме (разности) дифференциалов, т.е. d(u ± v) = du ± dv .

3) Дифференциал произведения находится по правилу: d(u ⋅ v) = du ⋅ v + u ⋅ dv .

4) d(C ⋅ u) = C ⋅ du , где C – константа.

5) Дифференциал дроби находится по правилу: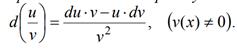

Рассмотрим дифференциал сложной функции y = f(ϕ(t)) .

Пусть функция x = ϕ(t) дифференцируемавточке t, функция y = f(x) дифференцируема в точке x = ϕ(t).

Тогда ∃ производные x ′ (t) и f ′ (x) и сложная функция y = f(ϕ(t)) имеет производную в точке t , причем y′ (t) = [f(ϕ(t))]′ = f ′ (x) ⋅ x′ (t)

Следовательно, функция y = f(ϕ(t)) дифференцируема в точке t

И ее дифференциал в этой точке равен

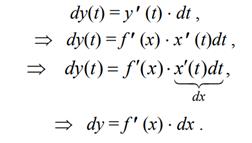
Сравним формулы (3) и (4):

(3):	dy = f ′ (x) ⋅ dx , где x – независимая переменная;
(4):	dy = f ′ (x) ⋅ dx , где x = ϕ(t) – функция.

Таким образом, формула (3) справедлива вне зависимости от того, является ли x независимым аргументом или функцией.

Поэтому формулу (3) называют инвариантной формой

Записи дифференциала.

Замечание. Формула dy = f ′(x) ⋅ Δx (2)

Не является инвариантной.

Действительно, для сложной функции y = f(ϕ(t)) имеем: dy(t) = y′ (t) ⋅ Δt = f ′(x) ⋅ x′ (t) ⋅ Δt . Но x′ (t) ⋅ Δt ≠ Δx , т.к.

Δx = dx + β(Δt) = x′ (t) ⋅ Δt + β(Δt) .