Вопросы к экзамену по математике. 1 семестр.

Аб-20-1, С-20-1

Вопросы к экзамену по математике. 1 семестр.

1. Определители 2-го порядка и их основные свойства.

2. Определители 3-го порядка. Миноры и алгебраические дополнения. Разложение определителя по строке, столбцу. Понятие об определителе высшего порядка.

3. Системы линейных уравнений, совместность и несовместность.

4. Правило Крамера.

5. Матрицы и операции над ними.

6. Обратная матрица. Теорема существования обратной матрицы, правило ее нахождения.

7. Матричная запись системы линейных уравнений и ее решение с помощью обратной матрицы.

8. Решение систем линейных уравнений методом Гаусса.

9. Понятие о ранге матрицы. Элементарные преобразования матрицы. Критерий совместности системы линейных уравнений, теорема Кронекера-Капелли.

10. Скалярные и векторные величины. Понятие вектора. Линейные операции над векторами.

11. Декартова система координат. Координаты вектора, длина, направляющие косинусы. Теорема о разложении вектора по базису.

12. Скалярное произведение векторов и его свойства.

13. Вычисление скалярного произведения через декартовы координаты векторов- множителей. Механический смысл скалярного произведения.

14. Векторное произведение векторов и его свойства. Геометрический смысл модуля векторного произведения.

15. Выражение векторного произведения через координаты перемножаемых векторов.

16. Смешанное произведение векторов и его свойства. Геометрический смысл смешанного произведения. Условие компланарности векторов.

17. Уравнение линии на плоскости. Уравнение прямой в 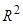, проходящей через данную точку перпендикулярно заданному вектору. Общее уравнение прямой, его частные случаи.

18. Каноническое уравнение прямой на плоскости. Уравнения прямой с угловым коэффициентом. Прямая "в отрезках".

19. Взаимное расположение прямых на плоскости. Угол между прямыми.

20. Полярная система координат. .

21. Нормальное уравнение прямой на плоскости. Расстояние от точки до прямой.

22. Кривые второго порядка на плоскости. Эллипс: определение, вывод канонического уравнения, исследование формы, эксцентриситет.

23. Гипербола: определение, каноническое уравнение, асимптоты, эксцентриситет.

24. Парабола: определение, вывод канонического уравнения.

25. Плоскость в пространстве 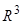. Уравнения плоскости: по точке и нормальному вектору, общее.

26. Уравнение плоскости, проходящей через три заданные точки. Плоскость "в отрезках".

27. Взаимное расположение плоскостей в пространстве. Нормальное уравнение плоскости. Расстояние от точки до плоскости.

28. Прямая в пространстве 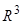. Канонические и параметрические уравнения прямой.

29. Взаимное расположение прямой и плоскости в 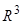, угол между прямой и плоскостью.

30. Множество комплексных чисел: основные понятия и определения. Геометрическое изображение комплексных чисел.

31. Действия над комплексными числами в алгебраическом виде.

32. Тригонометрическая форма и показательная формы комплексного числа.

Действия над комплексными числами в тригонометрическом виде.

33. Функция, область ее определения, способы задания. Понятие неявной, обратной, сложной функции.

34. Основные элементарные функции, их свойства и графики: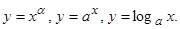

35. Тригонометрические и обратные тригонометрические функции, их свойства и графики.

36. Предел числовой последовательности. Теорема существования предела монотонной, ограниченной последовательности.

37. Предел функции в точке и на бесконечности. Односторонние пределы.

38. Бесконечно малые и бесконечно большие величины, их свойства.

39. Основные свойства предела. Признаки существования предела функции.

40. Первый замечательный предел, вывод. Второй замечательный предел.

41. Сравнение бесконечно малых. Эквивалентные бесконечно малые, их использование при вычислении пределов.

42. Непрерывность функции в точке. Свойства функций, непрерывных в точке. Непрерывность основных элементарных функций.

43. Свойства функций, непрерывных на отрезке.

44. Точки разрыва функции и их классификация.

45. Производная функции, ее механический и геометрический смыслы.

46. Дифференцирование, связь между дифференцируемостью и непрерывностью. Основные правила дифференцирования: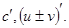

47. Основные правила дифференцирования: 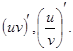Вывод формул.

48. Производная сложной и обратной функций.

49. Производная функций: 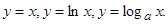Вывод формул.

50. Производные тригонометрических функций , вывод. Производная обратных тригонометрических функций.

51.Логарифмическое дифференцирование. Производная функций: 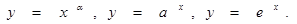Вывод формул.

52. Производные неявных и параметрически заданных функций. Производные высших порядков. Механический смысл производной второго порядка.

53. Дифференциал функции и его связь с производной. Геометрический смысл дифференциала.

54. Применение дифференциала в приближенных вычислениях.

55. Теоремы Ролля, Лагранжа и Коши.

56. Необходимое и достаточное условия возрастания и убывания функции.

57. Максимум и минимум функции. Необходимое и достаточное условия экстремума функции.

58. Выпуклость графика функции. Точки перегиба.

59. Асимптоты графика функции.

60. Общая схема исследования графика функции.

Литература.

1. Письменный, Д.Т. Конспект лекций по высшей математике: полный курс /

Д.Т. Письменный. – 9-е изд. – М.: Айрис-пресс, 2009.

2. Айдаркин, Д.В. Векторная алгебра и метод координат: учеб. пособие/ Д.В. Айдаркин, Л.И. Поленищенко. – Ульяновск: УВАУ ГА, 2007. – 116 с.

3. Пискунов, Н. С. Дифференциальное и интегральное исчисления: учебник для втузов : в 2 т. Т. 1 / Н. С. Пискунов. - изд. стер. - М.: Интеграл-Пресс, 2005. - 416 с.

4. Пискунов, Н. С. Дифференциальное и интегральное исчисления: учебное пособие для студ. втузов : в 2 т. Т. 2 / Н. С. Пискунов. - изд. стер. - М.: Интеграл-Пресс, 2005. - 544 с.

5. Математика: методические указания по изучению дисциплины / сост. Д. В. Айдаркин и др. - Ульяновск: УВАУ ГА (И), 2009. - 64 с.

6. Айдаркин, Д.В. Сборник задач и упражнений по векторной алгебре и методу координат: учеб. пособие/ Д.В. Айдаркин, Л.И. Поленищенко. – Ульяновск: УВАУ ГА (И), 2009. – 115 с.

7. Берман, Г. Н. Сборник задач по курсу математического анализа: учебное пособие / Г. Н. Берман. - 22-е изд., перераб. - СПб.: Изд-во "Профессия", 2008. - 432 с.

8. Клетеник, Д. В. Сборник задач по аналитической геометрии: учебное пособие для втузов / Д. В. Клетеник; под ред. Н. В. Ефимова. - 17-е изд., стер. - СПб.: Профессия, 2002. - 200 с.

9. Знаенко, Н.С. Опорные схемы по высшей математике: учебное пособие / Н.С. Знаенко. ‑ Ульяновск: УВАУ ГА (И), 2011. - 89 с.

10. Поленищенко Л.И. Сборник задач и упражнений по линейной алгебре: Учебное пособие. – 2-е изд., испр. и доп. / Л.И. Поленищенко, С.П. Никонова - Ульяновск: УВАУ ГА (И), 2011. - 63 с.